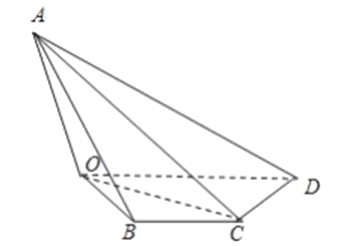
【题目】如图，四棱锥
中，已知平面
面
， 
， 
， 
， 
.
（1）求证：平面
平面
；
（2）直线
与平面
所成角为
，求二面角
的平面角的正切值.
【答案】（1）见解析；（2）
.
【解析】试题分析：（1）证明面面垂直，一般先在其中一个平面内寻找另一平面的一条垂线，再根据面面垂直判定定理进行论证.先利用平几知识计算出
，再根据条件面面垂直，利用面面垂直性质定理转化为线面垂直.（2）求二面角关键作出二面角的平面角，而作二面角的平面角，一般利用面面垂直性质定理得线面垂直，再结合三垂线定理及其逆定理可得，最后根据直角三角形求正切值.
试题解析：（1）证出
，
因为平面
, 
又
，所以平面
平面
（2）过
作
的垂线，垂足为
，则
过
作
的垂线，垂足为
，连
则
则
为所求
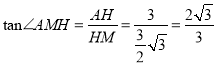
点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.
(1)证明线面、面面平行，需转化为证明线线平行.
(2)证明线面垂直，需转化为证明线线垂直.
(3)证明线线垂直，需转化为证明线面垂直.
科目：高中数学 来源： 题型：
【题目】记
表示
，
中的最大值，如
．已知函数
，
．
（1）设
，求函数
在
上零点的个数；
（2）试探讨是否存在实数
，使得
对
恒成立？若存在，求
的取值范围；若不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】总体由编号为00，01，02，…48，49的50个个体组成，利用下面的随机数表选取8个个体，选取方法是从随机数表第6行的第9列和第10列数字开始由左到右依次选取两个数字，则选出来的第8个个体的编号为（ ）
附：第6行至第9行的随机数表
2635 7900 3370 9160 1620 3882 7757 4950
3211 4919 7306 4916 7677 8733 9974 6732
2748 6198 7164 4148 7086 2888 8519 1620
7477 0111 1630 2404 2979 7991 9683 5125
A. 16 B. 19 C. 20 D. 38
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某商品每件成本5元，售价14元，每星期卖出75件．如果降低价格，销售量可以增加，且每星期多卖出的商品件数
与商品单价的降低值
（单位：元，
）的平方成正比，已知商品单价降低1元时，一星期多卖出5件．
（1）将一星期的商品销售利润
表示成的函数；
（2）如何定价才能使一个星期的商品销售利润最大？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
