
【题目】已知过点![]() 的动直线
的动直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,
两点,![]() 与直线
与直线![]() 相交于
相交于![]() .
.
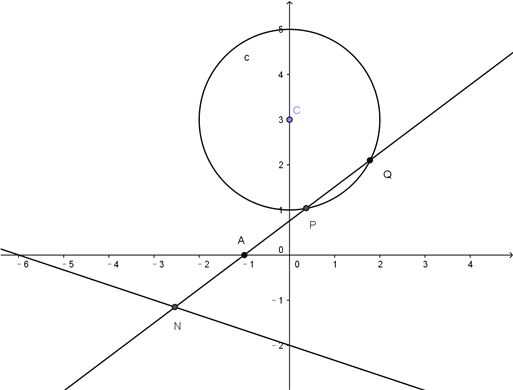
(1)当![]() 与
与![]() 垂直时,求直线
垂直时,求直线![]() 的方程,并判断圆心
的方程,并判断圆心![]() 与直线
与直线![]() 的位置关系;
的位置关系;
(2)当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】某企业开发一种新产品,现准备投入适当的广告费,对产品进行促销,在一年内,预计年销量Q(万件)与广告费x(万件)之间的函数关系为![]() ,已知生产此产品的年固定投入为3万元,每年产1万件此产品仍需要投入32万元,若年销售额为
,已知生产此产品的年固定投入为3万元,每年产1万件此产品仍需要投入32万元,若年销售额为![]() ,而当年产销量相等。
,而当年产销量相等。
(1)试将年利润P(万件)表示为年广告费x(万元)的函数;
(2)当年广告费投入多少万元时,企业年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨),一位居民的月用水量不超过
(吨),一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照![]() ,…,
,…,![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
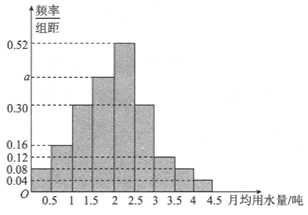
(1)求直方图中![]() 的值;
的值;
(2)若该市有110万居民,估计全市居民中月均用水量不低于3吨的人数,请说明理由;
(3)估计居民月均用水量的中位数(精确到0.01)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一批![]() 产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批
产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批![]() 产品所需原材料减少了
产品所需原材料减少了![]() 吨,且每吨原材料创造的利润提高了
吨,且每吨原材料创造的利润提高了![]() ;若将少用的
;若将少用的![]() 吨原材料全部用于生产公司新开发的
吨原材料全部用于生产公司新开发的![]() 产品,每吨原材料创造的利润为
产品,每吨原材料创造的利润为![]() 万元,其中a>0.
万元,其中a>0.
(1)若设备升级后生产这批A产品的利润不低于原来生产该批A产品的利润,求![]() 的取值范围;
的取值范围;
(2)若生产这批B产品的利润始终不高于设备升级后生产这批A产品的利润,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com