
【题目】如图,梯形![]() 中,
中,![]() 且
且![]() ,沿
,沿![]() 将梯形
将梯形![]() 折起,使得平面
折起,使得平面![]() ⊥平面
⊥平面![]()
![]() .
.
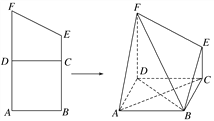
(1)证明:![]() ;
;
(2)求三棱锥![]() 的体积;
的体积;
(3)求直线![]() 。
。
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)取BF中点为M,AC与BD交点为O,连结MO,ME,由已知结合三角形中位线定理可得四边形OCEM为平行四边形,然后利用线面平行的判定得答案;
(2)由线面垂直的性质定理可得BC⊥平面DEF,然后把三棱锥D-BEF的体积转化为三棱锥B-DEF的体积求解.
(3)分析条件得![]() ,连结
,连结![]() ,
,![]() ,由
,由![]() 求解即可.
求解即可.
试题解析:
(1)证明 如图,取BF的中点![]() ,设
,设![]() 与
与![]() 交点为
交点为![]() ,连接
,连接![]() .
.
由题设知,![]() ,
,
∴![]() ,故四边形
,故四边形![]() 为平行四边形,
为平行四边形,
![]() 即
即![]() .
.
又![]() ,
,![]() ,
,
∴![]() .
.
(2)解 ∵平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]() ∩平面
∩平面![]() =
=![]() ,
,![]() ⊥
⊥![]() ,
,
∴![]() ⊥平面
⊥平面![]() .
.
∴三棱锥![]() 的体积为
的体积为
![]() .
.
(3)∵平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]() ∩平面
∩平面![]() =
=![]() ,又
,又![]()
![]() 又
又![]() ,
,
![]()
又在正方形![]() 中
中
![]()
![]()
连结![]() ,
,![]()
![]()
![]()
![]()
![]()


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】已知O为原点,A,B,C为平面内的三点.求证:
(1) 若A,B,C三点共线,则存在实数α,β,且α+β=1,![]()
(2) 若存在实数α,β,且α+β=1,使得![]() ,则A,B,C三点共线.
,则A,B,C三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品每件成本5元,售价14元,每星期卖出75件.如果降低价格,销售量可以增加,且每星期多卖出的商品件数![]() 与商品单价的降低值
与商品单价的降低值![]() (单位:元,
(单位:元,![]() )的平方成正比,已知商品单价降低1元时,一星期多卖出5件.
)的平方成正比,已知商品单价降低1元时,一星期多卖出5件.
(1)将一星期的商品销售利润![]() 表示成
表示成![]() 的函数;
的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,
, ![]() 且
且![]() 成等差数列。
成等差数列。
(1证明![]() 为等比数列,并求数列
为等比数列,并求数列![]() 的通项;
的通项;
(2)设![]() ,且
,且![]() ,证明
,证明![]() 。
。
(3)在(2)小问的条件下,若对任意的![]() ,不等式
,不等式![]() 恒成立,试求实数λ的取值范围.
恒成立,试求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在高为2的梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() ,
, ![]() ,垂足分别为
,垂足分别为![]() 、
、![]() 。已知
。已知![]() ,将梯形
,将梯形![]() 沿
沿![]() 、
、![]() 同侧折起,得空间几何体
同侧折起,得空间几何体![]() ,如图2。
,如图2。
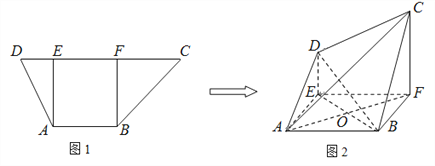
(1)若![]() ,证明:
,证明: ![]() ;
;
(2)若![]() ,证明:
,证明: ![]() ;
;
(3)在(1),(2)的条件下,求三棱锥![]() 的体积。
的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年12月16日,科幻片《侠盗一号》上映,上映至今,全球累计票房高达8亿美金.为了了解娄底观众的满意度,某影院随机调查了本市观看影片的观众,并用“10分制”对满意度进行评分,分数越高满意度越高,若分数不低于9分,则称该观众为“满意观众”.现从调查人群中随机抽取12名.如图所示的茎叶图记录了他们的满意度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶).
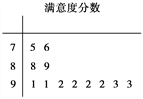
(1)求从这12人中随机选取1人,该人不是“满意观众”的概率;
(2)从本次所记录的满意度评分大于9.1的“满意观众”中随机抽取2人,求这2人得分不同的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com