
【题目】我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了了解老人们的健康状况,政府从老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行统计,样本分布被制作成如下图表:
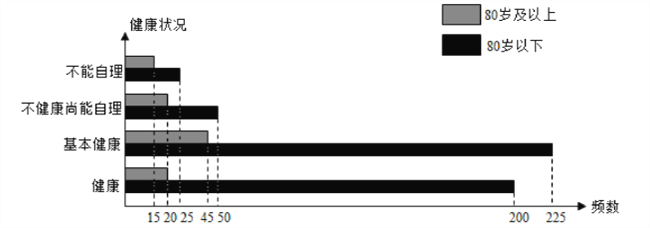
(1)若采用分层抽样的方法再从样本中的不能自理的老人中抽取8人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)估算该市80岁及以上长者占全市户籍人口的百分比;
(3)据统计该市大约有五分之一的户籍老人无固定收入,政府计划为这部分老人每月发放生活补贴,标准如下:
①80岁及以上长者每人每月发放生活补贴200元;
②80岁以下老人每人每月发放生活补贴120元;
③不能自理的老人每人每月额外发放生活补贴100元.
利用样本估计总体,试估计政府执行此计划的年度预算.(单位:亿元,结果保留两位小数)
【答案】(1)80岁及以上应抽取: ![]() 人,80岁以下应抽取:
人,80岁以下应抽取: ![]() 人;(2)
人;(2) ![]() ;(3)2.22亿元.
;(3)2.22亿元.
【解析】试题分析:(Ⅰ)从图表中求出不能自理的80岁及以上长者占比,由此能求出抽取16人中不能自理的80岁及以上长者人数为.
(Ⅱ)求出在600人中80岁及以上长者在老人中占比,用样本估计总体,能求出80岁及以上长者占户籍人口的百分比.
(Ⅲ)用样本估计总体,设任一户籍老人每月享受的生活补助为X元,则Xr可能取值为0,120,200,220,300,分别求出相应的概率,由此能求出随机变量X的分布列、EX,从而能估计政府执行此计划的年度预算.
试题解析:
(1)数据整理如下表:
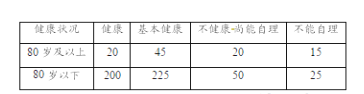
从图表中知不能自理的![]() 岁及以上长者比为:
岁及以上长者比为: ![]()
故抽取![]() 人中不能自理的
人中不能自理的![]() 岁及以上长者人数为
岁及以上长者人数为![]()
![]() 岁以下长者人数为
岁以下长者人数为![]() 人
人![]()
(2)在![]() 人中
人中![]() 岁及以上长者在老人中占比为:
岁及以上长者在老人中占比为: ![]()
用样本估计总体, ![]() 岁及以上长者共有
岁及以上长者共有![]() 万,
万,
![]() 岁及以上长者占户籍人口的百分比为
岁及以上长者占户籍人口的百分比为![]() %=
%=![]() %,
%,
(3)用样本估计总体,设任一户籍老人每月享受的生活补助为![]() 元,
元,
![]()
![]()
则随机变量的分布列为:
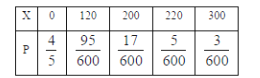
![]()
全市老人的总预算为![]() 元,
元,
政府执行此计划的年度预算约为![]() 亿元.
亿元.
求解离散型随机变量的数学期望的一般步骤为:
第一步是“判断取值”,即判断随机变量的所有可能取值,以及取每个值所表示的意义;
第二步是“探求概率”,即利用排列组合,枚举法,概率公式(常见的有古典概型公式、几何概率公式、互斥事件的概率和公式、独立事件的概率积,以及对立事件的概率公式等),求出随机变量取每个值时的概率;
第三步是“写分布列”,即按规范形式写出分布列,并注意用分布列的性质检验所求的分布列或某事件的概率是否正确;
第四步是“求期望值”,一般利用离散型随机变量的数学期望的定义求期望的值,对于有些实际问题中的随机变量,如果能够断定它服从某常见的典型分布(如二项分布![]() ,则此随机变量的期望可直接利用这种典型分布的期望公式(
,则此随机变量的期望可直接利用这种典型分布的期望公式(![]() )求得.因此,应熟记常见的典型分布的期望公式,可加快解题速度.
)求得.因此,应熟记常见的典型分布的期望公式,可加快解题速度.


科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2α﹣4cosα=0.已知直线l的参数方程为![]() (
(![]() 为参数),点M的直角坐标为
为参数),点M的直角坐标为![]() .
.
(1)求直线l和曲线C的普通方程;
(2)设直线l与曲线C交于A,B两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的长轴长为6,且椭圆
的长轴长为6,且椭圆![]() 与圆
与圆![]() :
: ![]() 的公共弦长为
的公共弦长为![]() .
.
(1)求椭圆![]() 的方程.
的方程.
(2)过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,
, ![]() ,试判断在
,试判断在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为以
为以![]() 为底边的等腰三角形.若存在,求出点
为底边的等腰三角形.若存在,求出点![]() 的横坐标的取值范围,若不存在,请说明理由.
的横坐标的取值范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断正确的是( )
A.![]() 或
或![]()
B.命题“若![]() 都是偶数,则
都是偶数,则![]() 是偶数”的逆否命题是“若
是偶数”的逆否命题是“若![]() 不是偶数,则
不是偶数,则![]() 都不是偶数”
都不是偶数”
C.若“![]() 或
或![]() ”为假命题,则“非
”为假命题,则“非![]() 且非
且非![]() ”是真命题
”是真命题
D.已知![]() 是实数,关于
是实数,关于![]() 的不等式
的不等式![]() 的解集是空集,必有
的解集是空集,必有![]() 且
且![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且在
,且在![]() 轴上的顶点分别为
轴上的顶点分别为![]() ,
,![]() .
.
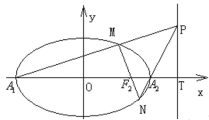
(1)求椭圆的方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为直线
为直线![]() 上异于点
上异于点![]() 的任一点,直线
的任一点,直线![]() 分别与椭圆交于
分别与椭圆交于![]() 点,试问直线
点,试问直线![]() 能否通过椭圆的焦点?若能,求出
能否通过椭圆的焦点?若能,求出![]() 的值,若不能,说明理由.
的值,若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法错误的是( )
A. 若“![]() ”为假命题,则p,q均为假命题
”为假命题,则p,q均为假命题
B. “ ![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C. “![]() ”的必要不充分条件是“
”的必要不充分条件是“![]() ”
”
D. 若命题p:![]() ,
,![]() ,则命题
,则命题![]() :
:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知AB丄平面BCD,M、N分别是AC、AD的中点,BC 丄 CD.

(1)求证:MN//平面BCD;
(2)若AB=1,BC=![]() ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 命题![]() “
“![]() ”,则
”,则![]() :“
:“![]() ”
”
B. 命题“若![]() ,则
,则![]() ”的否命题是真命题
”的否命题是真命题
C. 若![]() 为假命题,则
为假命题,则![]() 为假命题
为假命题
D. 若![]() 是
是![]() 的充分不必要条件,则
的充分不必要条件,则![]() 是
是![]() 的必要不充分条件
的必要不充分条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com