Question

【题目】以直角坐标系的原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρsin2α﹣4cosα=0．已知直线l的参数方程为（为参数），点M的直角坐标为.

（1）求直线l和曲线C的普通方程；

（2）设直线l与曲线C交于A，B两点，求.

Answer 1

【答案】(1)直线l的直角坐标方程为，曲线C的直角坐标方程为y2=4x；(2)8.

【解析】【试题分析】（1）对曲线极坐标方程两边乘以，化简为普通方程，对直线的参数方程，利用加减消元法消去，化为普通方程.（2）写出直线参数方程的标准形式，并代入曲线的普通方程，利用直线参数的几何意义和韦达定理，求得的值.

【试题解析】

（1）∵ρsin2α﹣2cosα=0，∴ρ2sin2α=4ρcosα，

∴曲线C的直角坐标方程为y2=4x．

由消去，得.

∴直线l的直角坐标方程为．

（2）点M（1，0）在直线l上，

设直线l的参数方程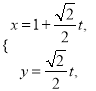（t为参数），A，B对应的参数为t1，t2．

将l的参数方程代入y2=4x，得.

于是， .

∴.