
| 温度x/℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
| 产卵数y/个 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
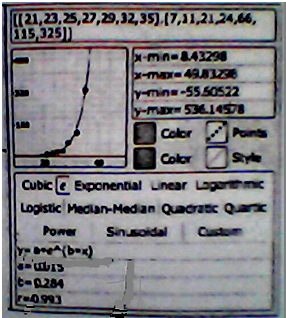
| ① | ② | ③ | ④ | ||||||||||||||||||||||||||
| 模型 | y=ax+b | y=aebx | y=ax2+c | y=ax3+bx2+cx+d | |||||||||||||||||||||||||
| 计算结果 |
|
|
|
|
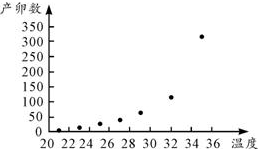
| x | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
| z | 1.946 | 2.398 | 3.045 | 3.178 | 4.190 | 4.745 | 5.784 |
| ∧ |
| z |
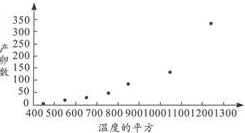
| t | 441 | 529 | 625 | 729 | 841 | 1 024 | 1 225 |
| y | 7 | 11 | 21 | 24 | 66 | 115 | 325 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 商店名称 | A | B | C | D | E |
| 销售额x/万元 | 3 | 5 | 6 | 7 | 9 |
| 利润额y/万元 | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 |
| y |
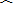 |
| a |
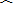 |
| a |
| x | 2 | 2.5 | 3 | 3.5 | 4 |
| y | 4 | 4.8 | 6.2 | 6.9 | 8.1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
A.
| B.
| ||||
C.
| D.
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| ? |
| y |
| A.废品率每增加1%,生铁成本增加3x元 |
| B.废品率每增加1%,生铁成本每吨增加3元 |
| C.废品率每增加1%,生铁成本增加234元 |
| D.废品率不变,生铁成本为234元 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.模型1 | B.模型2 | C.模型3 | D.模型4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 无效 | 有效 | 合计 | |
| 男性患者 | 15 | 35 | 50 |
| 女性患者 | 4 | 46 | 50 |
| 合计 | 19 | 81 | 100 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com