练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．观察下列事实：|x|+|y|≤1的不同整数解（x，y）的个数为5，|x|+|y|≤2 的不同整数解（x，y）的个数为13，|x|+|y|≤3的不同整数解（x，y）的个数为25 …．则|x|+|y|≤20的不同整数解（x，y）的个数为（　　）
    A．841B．761C．925D．941

    分析 观察可得不同整数解的个数相邻两项的差可以构成一个首项为4，公差为4的等差数列，进而可计算得结果．

    解答 解：∵|x|+|y|≤1的不同整数解（x，y）的个数为a1=5，
    |x|+|y|≤2 的不同整数解（x，y）的个数为a2=13，
    |x|+|y|≤3的不同整数解（x，y）的个数为a3=25，
    |x|+|y|≤4的不同整数解（x，y）的个数为a4=41，
    |x|+|y|≤5的不同整数解（x，y）的个数为a5=61，
    …．
    可得：a2-a1=8，
    a3-a2=12，
    a4-a3=16，
    a5-a4=20，
    则相邻两项的差可以构成一个首项为4，公差为4的等差数列，
    则a20-a19=80，
    累加得：a20-a1=8+12+16+…+80=836，
    故a20=841，
    故选：A

    点评 归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    15．已知空间点A（x，1，2）和点B（2，3，4），且|AB|=2$\sqrt{6}$，则点A的坐标为（6，1，2）或（-2，1，2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．在△ABC中，角A、B、C所对的边分别为a、b、c，若角$C＞\frac{π}{3}$，asin2C=bsinA，则下列结论正确的有（　　）个               
    ①一定是锐角三角形；
    ②一定是等腰三角形；
    ③可能是等腰直角三角形；
    ④可能是等边三角形．
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．等差数列{an}中，a3+a9=a5，则S13=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．若-$\frac{π}{2}$＜α＜β＜$\frac{π}{2}$，则α-β的取值范围是（　　）
    A．（-π，π）B．（0，π）C．（-π，0）D．{0}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．若奇函数f（x）的定义域为R，且f（x+4）=f（x），当x∈（4，6]时f（x）=2x+1，求f（x）在区间[-2，0）上的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．设x，y，z为正数，xyz=1，求3x+4y+5z的最小值，以及x，y，z为何值时，3x+4y+5z达到最小值？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

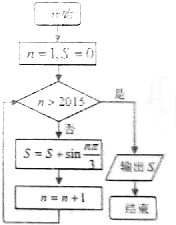    14．执行如图所示程序框图，则其结果输出S为（　　）
    A．0B．$\frac{\sqrt{3}}{3}$C．$\sqrt{3}$D．$\frac{4\sqrt{3}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知x2+y2+x+$\sqrt{3}$y+tanθ=0（-$\frac{π}{2}$＜θ＜$\frac{π}{2}$）表示圆，则θ的取值范围为$（-\frac{π}{2}，\frac{π}{4}）$．

    查看答案和解析>>

    同步练习册答案