
已知函数f(x)=sin sin(
sin(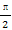 +
+ ).
).
(1)求函数f(x)在[-π,0]上的单调区间.
(2)已知角α满足α∈(0,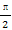 ),2f(2α)+4f(
),2f(2α)+4f(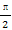 -2α)=1,求f(α)的值.
-2α)=1,求f(α)的值.
(1) 单调递减区间为[-π,- ],单调递增区间为[-
],单调递增区间为[- ,0]
,0]
(2) 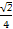
【解析】【思路点拨】(1)利用诱导公式及倍角公式化简f(x)的解析式后可求.
(2)利用已知将条件代入,整理成单角α的三角函数关系式后可解.
解:f(x)=sin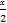 sin(
sin( +
+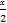 )
)
=sin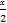 cos
cos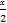 =
=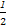 sinx.
sinx.
(1)函数f(x)的单调递减区间为[-π,- ],单调递增区间为[-
],单调递增区间为[- ,0].
,0].
(2)2f(2α)+4f( -2α)=1
-2α)=1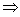 sin2α+2sin(
sin2α+2sin( -2α)=1
-2α)=1
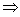 2sinαcosα+2(cos2α-sin2α)=1
2sinαcosα+2(cos2α-sin2α)=1
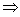 cos2α+2sinαcosα-3sin2α=0
cos2α+2sinαcosα-3sin2α=0
⇒(cosα+3sinα)(cosα-sinα)=0.
∵α∈(0, ),
),
∴cosα-sinα=0⇒tanα=1得α= ,故sinα=
,故sinα= ,
,
∴f(α)=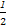 sinα=
sinα=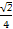 .
.


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十五第四章第一节练习卷(解析版) 题型:选择题
在△ABC中,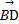 =2
=2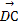 ,
, =m
=m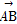 +n
+n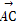 ,则
,则 的值为( )
的值为( )
(A)2(B) (C)3(D)
(C)3(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十三第三章第七节练习卷(解析版) 题型:解答题
在△ABC中,a,b,c分别为角A,B,C的对边.已知a=1,b=2,sinC=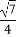 (其中C为锐角).
(其中C为锐角).
(1)求边c的值.
(2)求sin(C-A)的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十七第四章第三节练习卷(解析版) 题型:选择题
已知a,b,c为△ABC的三个内角A,B,C的对边,向量m=(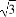 ,-1),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角A,B的大小分别为( )
,-1),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角A,B的大小分别为( )
(A)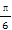 ,
,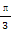 (B)
(B)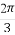 ,
,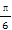
(C)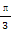 ,
,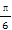 (D)
(D)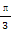 ,
,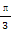
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十七第四章第三节练习卷(解析版) 题型:选择题
已知非零向量a,b满足向量a+b与向量a-b的夹角为 ,那么下列结论中一定成立的是( )
,那么下列结论中一定成立的是( )
(A)a=b(B)|a|=|b|
(C)a⊥b(D)a∥b
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十一第三章第五节练习卷(解析版) 题型:选择题
设sin( +θ)=
+θ)= ,则sin2θ等于( )
,则sin2θ等于( )
(A)- (B)
(B)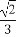 (C)
(C) (D)
(D)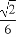
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十第五章第一节练习卷(解析版) 题型:解答题
设数列{an}前n项和为Sn,数列{Sn}的前n项和为Tn,满足Tn=2Sn-n2,n∈N*.
(1)求a1的值.
(2)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十四第五章第五节练习卷(解析版) 题型:解答题
甲、乙两人用农药治虫,由于计算错误,在A,B两个喷雾器中分别配制成12%和6%的药水各10千克,实际要求两个喷雾器中的农药的浓度是一样的,现在只有两个能容纳1千克药水的药瓶,他们从A,B两个喷雾器中分别取1千克的药水,将A中取得的倒入B中,B中取得的倒入A中,这样操作进行了n次后,A喷雾器中药水的浓度为an%,B喷雾器中药水的浓度为bn%.
(1)证明an+bn是一个常数.
(2)求an与an-1的关系式.
(3)求an的表达式.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十八第六章第四节练习卷(解析版) 题型:选择题
小王从甲地到乙地往返的时速分别为a和b(a<b),其全程的平均时速为v,则( )
(A)a<v<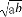 (B)v=
(B)v=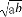
(C)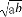 <v<
<v<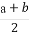 (D)v=
(D)v=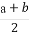
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com