练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知直线2x＋(y－3)m－4＝0(m∈R)恒过定点P，若点P平分圆x2＋y2－2x－4y－4＝0的弦MN，则弦MN所在直线的方程是(　　)

    A．x＋y－5＝0    B．x＋y－3＝0  C．x－y－1＝0    D．x－y＋1＝0


    A


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在各项均为正数的等差数列{an}中，对任意的n∈N*都有a1＋a2＋…＋an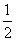＝anan＋1.

    (1)求数列{an}的通项an；

    (2)设数列{bn}满足b1＝1，bn＋1－bn＝2an，求证：对任意的n∈N*都有bnbn＋2<b.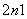

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在如图所示的数表中，第i行第j列的数记为a(i，j)，且a(1，j)＝2j－1，a(i,1)＝i，a(i＋1，j＋1)＝a(i，j)＋a(i＋1，j)，则此数表中若记第3行的数3,5,8,13，22，…，为数列{bn}，则{bn}的通项公式为________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在直角坐标系xOy中，已知A(－1,0)，B(0,1)，则满足|PA|2－|PB|2＝4且在圆x2＋y2＝4上的点P的个数为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    过P(2,0)的直线l被圆(x－2)2＋(y－3)2＝9截得的线段长为2时，直线l的斜率为(　　)

    A．±  B．±  C．±1  D．±

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在平面直角坐标系xOy中，若圆x2＋(y－1)2＝4上存在A，B两点关于点P(1,2)成中心对称，则直线AB的方程为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知△ABC的两顶点坐标A(－1,0)，B(1,0)，圆E是△ABC的内切圆，在边AC，BC，AB上的切点分别为P，Q，R，|CP|＝1(从圆外一点到圆的两条切线长相等)，动点C的轨迹为曲线M.

    (1)求曲线M的方程；

    (2)设直线BC与曲线M的另一交点为D，当点A在以线段CD为直径的圆上时，求直线BC的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一次考试中，五名学生的数学、物理成绩如下表所示：

    学生

    A1

    A2

    A3

    A4

    A5

    数学成绩x/分

    89

    91

    93

    95

    97

    物理成绩y/分

    87

    89

    89

    92

    93

    (1)要从5名学生中选2人参加一项活动，求选中的学生中至少有一人的物理成绩高于90分的概率；

    (2)根据上表数据，用变量y与x的相关系数和散点图说明物理成绩y与数学成绩x之间线性相关关系的强弱．如果具有较强的线性相关关系，求y与x的线性回归方程(系数精确到0.01)；如果不具有线性相关关系，请说明理由．

    参考公式：

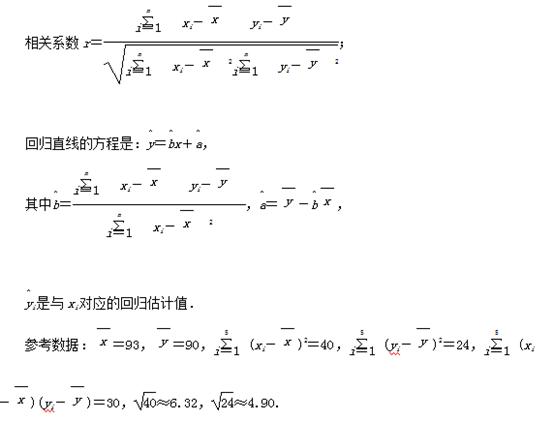
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某企业有甲、乙两个研发小组，他们研发新产品成功的概率分别为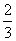和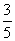，现安排甲组研发新产品A，乙组研发新产品B，设甲、乙两组的研发相互独立．

    (1)求至少有一种新产品研发成功的概率；

    (2)若新产品A研发成功，预计企业可获利润120万元；若新产品B研发成功，预计企业可获利润100万元，求该企业可获利润的分布列和数学期望．

    查看答案和解析>>

    同步练习册答案