
在各项均为正数的等差数列{an}中,对任意的n∈N*都有a1+a2+…+an=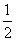 anan+1.
anan+1.
(1)求数列{an}的通项an;
(2)设数列{bn}满足b1=1,bn+1-bn=2an,求证:对任意的n∈N*都有bnbn+2<b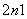 .
.
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
一个正方体纸盒展开后如图,在原正方体纸盒中有下列结论:
①AB⊥EF ②AB与CM成60° ③EF与MN是异面直线 ④MN∥CD
其中正确的是 ( )
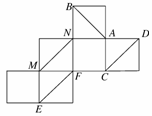
A.①② B.③④ C.②③ D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=2x2-ax+ln x在其定义域上不单调,则实数a的取值范围是( )
A.(-∞,4] B.(-∞,4)
C.(4,+∞) D.[4,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线2x+(y-3)m-4=0(m∈R)恒过定点P,若点P平分圆x2+y2-2x-4y-4=0的弦MN,则弦MN所在直线的方程是( )
A.x+y-5=0 B.x+y-3=0 C.x-y-1=0 D.x-y+1=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com