
数列{an}满足a1=2,an= ,其前n项积为Tn,则T2 014=( )
,其前n项积为Tn,则T2 014=( )
A.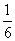 B.-
B.-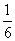
C.6 D.-6
科目:高中数学 来源: 题型:
设有关于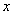 的一元二次方程
的一元二次方程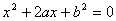
(1)若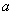 是从0,1,2,3四个数中任意取一个数,
是从0,1,2,3四个数中任意取一个数,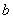 是从0,1,2三个数中任意取一个,求上述方程有实根的概率
是从0,1,2三个数中任意取一个,求上述方程有实根的概率
(2)若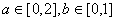 ,求上述方程有实根的概率
,求上述方程有实根的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
在各项均为正数的等差数列{an}中,对任意的n∈N*都有a1+a2+…+an=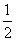 anan+1.
anan+1.
(1)求数列{an}的通项an;
(2)设数列{bn}满足b1=1,bn+1-bn=2an,求证:对任意的n∈N*都有bnbn+2<b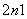 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC= AD=1,CD=
AD=1,CD=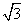 .
.
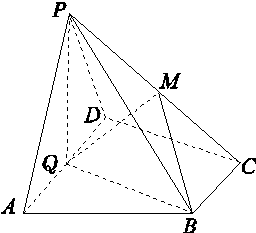
(1)求证:平面PQB⊥平面PAD;
(2)若M为棱PC的中点,求异面直线AP与BM所成角的余弦值;
(3)若二面角M-BQ-C的大小为30°,求QM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com