
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC= AD=1,CD=
AD=1,CD=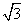 .
.
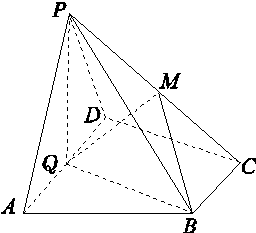
(1)求证:平面PQB⊥平面PAD;
(2)若M为棱PC的中点,求异面直线AP与BM所成角的余弦值;
(3)若二面角M-BQ-C的大小为30°,求QM的长.
解:(1)证明:证法一:∵AD∥BC,BC= AD,Q为AD的中点,
AD,Q为AD的中点,
∴四边形BCDQ为平行四边形,
∴CD∥BQ.
∵∠ADC=90°,
∴∠AQB=90°,
即QB⊥AD.
又∵平面PAD⊥平面ABCD,
且平面PAD∩平面ABCD=AD,
∴BQ⊥平面PAD.
∵BQ⊂平面PQB,
∴平面PQB⊥平面PAD.
证法二:∵AD∥BC,BC= AD,Q为AD的中点,
AD,Q为AD的中点,
∴BC∥DQ且BC=DQ,
∴四边形BCDQ为平行四边形,∴CD∥BQ.
∵∠ADC=90°,
∴∠AQB=90°,即QB⊥AD.
∵PA=PD,∴PQ⊥AD.
∵PQ∩BQ=Q,
∴AD⊥平面PBQ.
∵AD⊂平面PAD,∴平面PQB⊥平面PAD.
(2)∵PA=PD,Q为AD的中点,
∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,∴PQ⊥平面ABCD.
如图,以Q为原点建立空间直角坐标系Q-xyz,
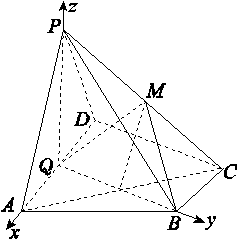
则Q(0,0,0),A(1,0,0),P(0,0,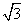 ),B(0,
),B(0,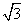 ,0),C(-1,
,0),C(-1,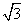 ,0).
,0).
∵M是PC的中点,
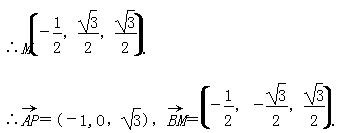 设异面直线AP与BM所成的角为θ,
设异面直线AP与BM所成的角为θ,
则cos θ=|cos〈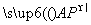 ,
,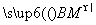 〉|
〉|
=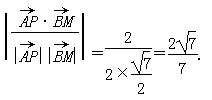
∴异面直线AP与BM所成角的余弦值为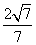 .
.
(3)由(2)知平面BQC的一个法向量为n=(0,0,1).
 ∵二面角M-BQ-C的大小为30°,
∵二面角M-BQ-C的大小为30°,
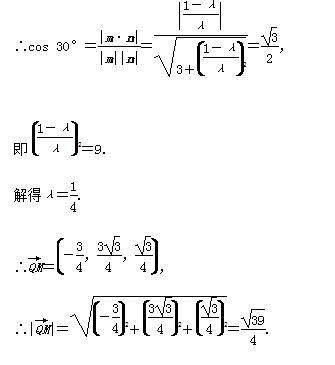 即QM的长为
即QM的长为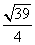 .
.


科目:高中数学 来源: 题型:
已知点P是以F1,F2为焦点的椭圆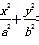 =1(a>b>0)上一点,若PF1⊥PF2,tan ∠PF2F1=2,则椭圆的离心率e=( )
=1(a>b>0)上一点,若PF1⊥PF2,tan ∠PF2F1=2,则椭圆的离心率e=( )
A.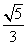 B.
B.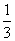 C.
C.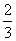 D.
D.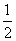
查看答案和解析>>
科目:高中数学 来源: 题型:
如图是2013年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和众数依次为( )
A.85,84 B.84,85
C.86,84 D.84,86
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com