练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知平行四边形ABCD中，＝(2,8)，＝(－3,4)，对角线AC与BD相交于点M，则的坐标为(　　)


    B

    [解析]　由题意可知，，故选B.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设F1、F2为椭圆+y2＝1的两焦点，P在椭圆上，当△F1PF2面积为1时， 的值为（    ）

        A．0             B．1             C．2             D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝ex(sin x－cos x)(0≤x≤2 012π)，则函数f(x)的各极小值之和为(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设正方体ABCD－A1B1C1D1的棱长为2，则点D1到平面A1BD的距离是(　　)

    A.                                  B.

    C.                                 D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在四棱锥P－ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC＝90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA＝PD＝2，BC＝AD＝1，CD＝.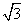

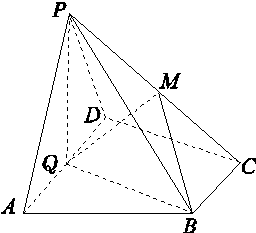
    (1)求证：平面PQB⊥平面PAD；

    (2)若M为棱PC的中点，求异面直线AP与BM所成角的余弦值；

    (3)若二面角M－BQ－C的大小为30°，求QM的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在平面直角坐标系xOy中，Ω是一个平面点集，如果存在非零平面向量a，对于任意点P∈Ω，都有点Q∈Ω，使得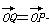＋a，则称a为平面点集Ω的一个向量周期．现有以下四个命题：

    ①若平面点集Ω存在向量周期a，则ka(k∈Z，k≠0)也是Ω的向量周期；

    ②若平面点集Ω形成的平面图形的面积是一个非零常数，则Ω不存在向量周期；

    ③若平面点集Ω＝{(x，y)|x＞0，y＞0}，则b＝(－1,2)为Ω的一个向量周期；

    ④若平面点集Ω＝{(x，y)|y＝|sin x|－|cos x|}，则c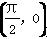＝为Ω的一个向量周期．

    其中真命题的个数是(　　)

    A．1  B．2  C．3  D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    给出30个数：1,2,4,7,11,16，…，要计算这30个数的和，如图给出了该问题的程序框图，那么框图中判断框①处和执行框②处可分别填入(　　)

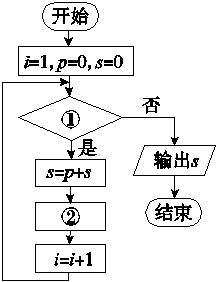
    A．i≤30？和p＝p＋i－1   

    B．i≤31？和p＝p＋i＋1

    C．i≤31？和p＝p＋i   

    D．i≤30？和p＝p＋i

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    数列{an}满足a1＝a2＝1，an＋an＋1＋an＋2＝cos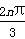(n∈N*)，若数列{an}的前n项和为Sn，则S2 013的值为(　　)

    A．2 013  B．671  C．－671  D．－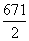

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    为了估计某水池中鱼的尾数，先从水池中捕出2 000尾鱼，并给每尾鱼做上标记(不影响存活)，然后放回水池，经过适当的时间，再从水池中捕出500尾鱼，其中有标记的鱼为40尾，根据上述数据估计该水池中鱼的尾数为(　　)

    A．10 000  B．20 000  C．25 000  D．30 000

    查看答案和解析>>

    同步练习册答案