
设正方体ABCD-A1B1C1D1的棱长为2,则点D1到平面A1BD的距离是( )
A.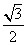 B.
B.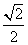
C.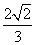 D.
D.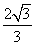
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
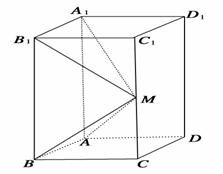
如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点.
(1)求异面直线A1M和C1D1所成的角的正切值;
(2)求平面ABM与平面A1B1M.所成的二面角大小
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=ex-x-1,g(x)=x2eax.
(1)求f(x)的最小值;
(2)求g(x)的单调区间;
(3)当a=1时,对于在(0,1)中的任一个常数m,是否存在正数x0使得f(x0)>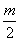 g(x0)成立?如果存在,求出符合条件的一个x0;否则说明理由.
g(x0)成立?如果存在,求出符合条件的一个x0;否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
设等差数列{an}满足公差d∈N*,an∈N*,且数列{an}中任意两项之和也是该数列的一项.若a1=35,则d的所有可能取值之和为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在几何体ABCDE中,AB=AD=BC=DC=2,AE=2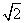 ,AB⊥AD,且AE⊥平面ABD,平面CBD⊥平面ABD.
,AB⊥AD,且AE⊥平面ABD,平面CBD⊥平面ABD.
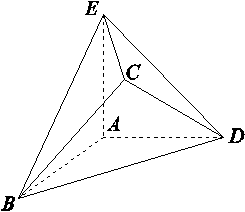
(1)求证:AB∥平面CDE;
(2)求二面角A-EC-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
设{an}是集合{2s+2t|0≤s<t且s,t∈Z}中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…,将数列{an}各项按照上小下大、左小右大的原则写成如下的三角形数表:
3
5 6
9 10 12
…
则a99等于( )
A.8 320 B.16 512 C.16 640 D.8 848
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面直角坐标系xOy中,已知点P(3,0)在圆C:x2+y2-2mx-4y+m2-28=0内,动直线AB过点P且交圆C于A,B两点,若△ABC的面积的最大值为16,则实数m的取值范围为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com