练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设{an}是集合{2s＋2t|0≤s＜t且s，t∈Z}中所有的数从小到大排列成的数列，即a1＝3，a2＝5，a3＝6，a4＝9，a5＝10，a6＝12，…，将数列{an}各项按照上小下大、左小右大的原则写成如下的三角形数表：

    3

    5    6

    9   10    12

    …

    则a99等于(　　)

    A．8 320  B．16 512  C．16 640  D．8 848


    B

    [解析]　用(s，t)表示2s＋2t，则三角形数表可表示为

    第一行　3(0,1)

    第二行　5(0,2)　6(1,2)

    第三行　9(0,3)　10(1,3)　12(2,3)

    第四行　17(0,4)　18(1,4)　20(2,4)　24(3,4)

    第五行　33(0,5)　34(1,5)　36(2,5)　40(3,5)　48(4,5)

    …

    因为99＝(1＋2＋3＋4＋…＋13)＋8，所以a99＝(7,14)＝27＋214＝16 512，故选B.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设函数f(x)＝ln(1＋x)，g(x)＝xf′(x)，x≥0，其中f′(x)是f(x)的导函数．若f(x)≥ag(x)恒成立，则实数a的取值范围是(　　)

    A．(－1，＋∞)                          B．(0，＋∞) 

    C．(－∞，0)                            D．(－∞，1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设正方体ABCD－A1B1C1D1的棱长为2，则点D1到平面A1BD的距离是(　　)

    A.                                  B.

    C.                                 D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在平面直角坐标系xOy中，Ω是一个平面点集，如果存在非零平面向量a，对于任意点P∈Ω，都有点Q∈Ω，使得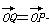＋a，则称a为平面点集Ω的一个向量周期．现有以下四个命题：

    ①若平面点集Ω存在向量周期a，则ka(k∈Z，k≠0)也是Ω的向量周期；

    ②若平面点集Ω形成的平面图形的面积是一个非零常数，则Ω不存在向量周期；

    ③若平面点集Ω＝{(x，y)|x＞0，y＞0}，则b＝(－1,2)为Ω的一个向量周期；

    ④若平面点集Ω＝{(x，y)|y＝|sin x|－|cos x|}，则c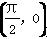＝为Ω的一个向量周期．

    其中真命题的个数是(　　)

    A．1  B．2  C．3  D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    给出30个数：1,2,4,7,11,16，…，要计算这30个数的和，如图给出了该问题的程序框图，那么框图中判断框①处和执行框②处可分别填入(　　)

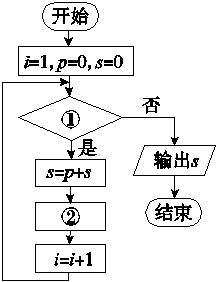
    A．i≤30？和p＝p＋i－1   

    B．i≤31？和p＝p＋i＋1

    C．i≤31？和p＝p＋i   

    D．i≤30？和p＝p＋i

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    请阅读下列材料：若两个正实数a1，a2满足a＋a＝1，那么a1＋a2≤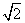.证明：构造函数f(x)＝(x－a1)2＋(x－a2)2＝2x2－2(a1＋a2)x＋1，因为对一切实数x，恒有f(x)≥0，所以Δ≤0，从而得4(a1＋a2)2－8≤0，所以a1＋a2≤.

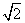    根据上述证明方法，若n个正实数满足a＋a＋…＋a＝1时，你能得到的结论为________．(不必证明)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    数列{an}满足a1＝a2＝1，an＋an＋1＋an＋2＝cos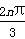(n∈N*)，若数列{an}的前n项和为Sn，则S2 013的值为(　　)

    A．2 013  B．671  C．－671  D．－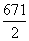

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点A(－3,0)，B(0,3)，若点P在圆x2＋y2－2x＝0上运动，则△PAB面积的最小值为(　　)

    A．6    B．6    C．6＋     D．6－

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设 且,则的最小值为       （   ）

       A．12            B．15               C．16               D．-16

    查看答案和解析>>

    同步练习册答案