
如图,在几何体ABCDE中,AB=AD=BC=DC=2,AE=2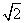 ,AB⊥AD,且AE⊥平面ABD,平面CBD⊥平面ABD.
,AB⊥AD,且AE⊥平面ABD,平面CBD⊥平面ABD.
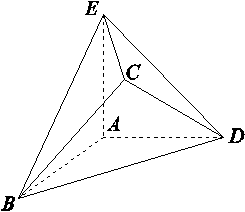
(1)求证:AB∥平面CDE;
(2)求二面角A-EC-D的余弦值.
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
已知各项不为0的等差数列{an}满足a4-2a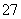 +3a8=0,数列{bn}是等比数列,且b7=a7,则b2b12等于( )
+3a8=0,数列{bn}是等比数列,且b7=a7,则b2b12等于( )
A.1 B.2
C.4 D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
一个几何体的三视图如图所示,正视图和侧视图都是等边三角形.若该几何体的四个顶点在空间直角坐标系O-xyz中的坐标分别是(0,0,0),(2,0,0),(2,2,0),(0,2,0),则第五个顶点的坐标可能为( )

A.(1,1,1) B.(1,1,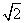 )
)
C.(1,1,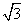 ) D.(2,2,
) D.(2,2,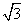 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面直角坐标系xOy中,Ω是一个平面点集,如果存在非零平面向量a,对于任意点P∈Ω,都有点Q∈Ω,使得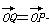 +a,则称a为平面点集Ω的一个向量周期.现有以下四个命题:
+a,则称a为平面点集Ω的一个向量周期.现有以下四个命题:
①若平面点集Ω存在向量周期a,则ka(k∈Z,k≠0)也是Ω的向量周期;
②若平面点集Ω形成的平面图形的面积是一个非零常数,则Ω不存在向量周期;
③若平面点集Ω={(x,y)|x>0,y>0},则b=(-1,2)为Ω的一个向量周期;
④若平面点集Ω={(x,y)|y=|sin x|-|cos x|},则c=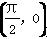 为Ω的一个向量周期.
为Ω的一个向量周期.
其中真命题的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
请阅读下列材料:若两个正实数a1,a2满足a +a
+a =1,那么a1+a2≤
=1,那么a1+a2≤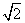 .证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以Δ≤0,从而得4(a1+a2)2-8≤0,所以a1+a2≤
.证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以Δ≤0,从而得4(a1+a2)2-8≤0,所以a1+a2≤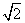 .
.
根据上述证明方法,若n个正实数满足a +a
+a +…+a
+…+a =1时,你能得到的结论为________.(不必证明)
=1时,你能得到的结论为________.(不必证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
某产品在某零售摊位上的零售价x(元)与每天的销售量y(个)统计如下表:
| x | 16 | 17 | 18 | 19 |
| y | 50 | 41 | 34 | 31 |
据上表可得回归直线方程 =bx+a中的b=-4,据此模型预计零售价定为15元时,销售量为( )
=bx+a中的b=-4,据此模型预计零售价定为15元时,销售量为( )
A.48 B.49 C.50 D.51
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com