
一个几何体的三视图如图所示,正视图和侧视图都是等边三角形.若该几何体的四个顶点在空间直角坐标系O-xyz中的坐标分别是(0,0,0),(2,0,0),(2,2,0),(0,2,0),则第五个顶点的坐标可能为( )

A.(1,1,1) B.(1,1,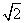 )
)
C.(1,1,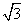 ) D.(2,2,
) D.(2,2,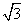 )
)
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
设等差数列{an}满足公差d∈N*,an∈N*,且数列{an}中任意两项之和也是该数列的一项.若a1=35,则d的所有可能取值之和为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在几何体ABCDE中,AB=AD=BC=DC=2,AE=2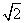 ,AB⊥AD,且AE⊥平面ABD,平面CBD⊥平面ABD.
,AB⊥AD,且AE⊥平面ABD,平面CBD⊥平面ABD.
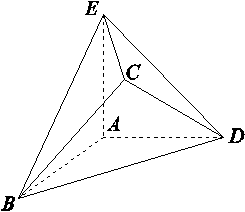
(1)求证:AB∥平面CDE;
(2)求二面角A-EC-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
圆心在曲线y= (x>0)上,与直线2x+y+1=0相切,且面积最小的圆的方程为( )
(x>0)上,与直线2x+y+1=0相切,且面积最小的圆的方程为( )
A.(x-2)2+(y-1)2=25 B.(x-2)2+(y-1)2=5
C.(x-1)2+(y-2)2=25 D.(x-1)2+(y-2)2=5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com