练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

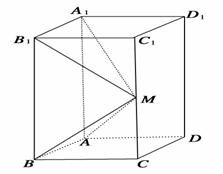
    如图所示，在长方体ABCD－A1B1C1D1中，AB＝AD＝1，AA1＝2，M是棱CC1的中点．

    (1)求异面直线A1M和C1D1所成的角的正切值；

    (2)求平面ABM与平面A1B1M.所成的二面角大小


    解：

    （1)如图，因为C1D1∥B1A1，所以∠MA1B1为异面直线A1M与C1D1所成的角．

    因为A1B1⊥平面BCC1B1，所以∠A1B1M＝90°，

    而A1B1＝1，B1M＝，故

    tan∠MA1B1＝＝.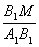

    即异面直线A1M和C1D1所成的角的正切值为.

    (2)由A1B1⊥平面BCC1B1，BM⊂平面BCC1B1，得

    A1B1⊥BM①

    由(1)知，B1M＝，

    又BM＝，B1B＝2，

    所以B1M2＋BM2＝B1B2，从而BM⊥B1M②

    又A1B1∩B1M＝B1，∴BM⊥平面A1B1M，而BM⊂平面ABM，

    因此平面ABM⊥平面A1B1M.故平面ABM与平面A1B1M.所成的二面角大小为：900


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


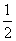    用min{a，b}表示a，b两个数中的较小的数，设f(x)＝min{x2，}，那么由函数y＝f(x)的图象、x轴、直线x＝和直线x＝4所围成的封闭图形的面积为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    计算的值为                               （   ）

      A、    B、        C、          D、

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知 a=log0.70.8，b=log1.10.9，C=1.10.9,那么                              （    ）

    A. a<b<c           B. a<c<b        C. b<a<c       D. c<a<b

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点P为直线上一点，P到直线的距离与原点到这条直线的距离相等，则点P的坐标是           

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数的零点所在的大致区间是 (   )

       A .              B.            C. 和       D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设F1、F2为椭圆+y2＝1的两焦点，P在椭圆上，当△F1PF2面积为1时， 的值为（    ）

        A．0             B．1             C．2             D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝ln(1＋x)，g(x)＝xf′(x)，x≥0，其中f′(x)是f(x)的导函数．若f(x)≥ag(x)恒成立，则实数a的取值范围是(　　)

    A．(－1，＋∞)                          B．(0，＋∞) 

    C．(－∞，0)                            D．(－∞，1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设正方体ABCD－A1B1C1D1的棱长为2，则点D1到平面A1BD的距离是(　　)

    A.                                  B.

    C.                                 D.

    查看答案和解析>>

    同步练习册答案