练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

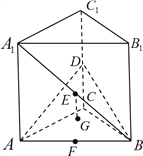
    【题目】如图，在直三棱柱中，底面是等腰直角三角形， ，侧棱，点分别为棱的中点， 的重心为，直线垂直于平面.

    （1）求证：直线平面；

    （2）求二面角的余弦.

    【答案】(1)证明见解析；(2) .

    【解析】试题分析：（1）证线面平行，直接找线线平行即可，构造平行四边形，证明平行于DE，即可得到线线平行，进而得到线面平行。（2）建系，分别求出两个半平面的法向量，根据公式得到法向量的夹角，从而得到二面角的大小。

    (1) 连结 ，则在三角形中为中位线，于是，

    因为为中点，所以平行且等于. 所以在平行四边形中， 平行于

    因为在平面 上，所以平行于平面

    （2）分别以为轴建立空间直角坐标系

    设，则

    因为垂直于平面，所以有，

    解得，所以

    面的法向量，面的法向量为

    所以

    结合图形知，二面角的预先为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）求函数的单调区间；

    （2）若关于的方程有实数根，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（）．　

    （1）若在其定义域内单调递增，求实数的取值范围；

    （2）若，且有两个极值点， （），求取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在数列{an}中，a1=1，an+1= （n=1，2，3，…），
    （1）计算a1 ， a2 ， a3 ， a4；
    （2）猜想an的表达式，并用数学归纳法证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，若关于的方程恰好有 4 个不相等的实数解，则实数的取值范围为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆E： =1（a＞b＞0）上任意一点到两焦点距离之和为 ，离心率为 ，左、右焦点分别为F1 ， F2 ， 点P是右准线上任意一点，过F2作直线PF2的垂线F2Q交椭圆于Q点．
    （1）求椭圆E的标准方程；
    （2）证明：直线PQ与直线OQ的斜率之积是定值；
    （3）证明：直线PQ与椭圆E只有一个公共点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在10个球中有6个红球和4个白球（各不相同），不放回地依次摸出2个球，在第一次摸出红球的条件下，第2次也摸到红球的概率为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= sin2x﹣cos2x，有下列四个结论：①f（x）的最小正周期为π；②f（x）在区间[﹣ ， ]上是增函数；③f（x）的图象关于点（ ，0）对称；④x= 是f（x）的一条对称轴．其中正确结论的个数为（ ）
    A.1
    B.2
    C.3
    D.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数F（x）=lnx（x＞1）的图象与函数G（x）的图象关于直线y=x对称，若函数f（x）=（k﹣1）x﹣G（﹣x）无零点，则实数k的取值范围是（ ）
    A.（1﹣e，1）
    B.（1﹣e，∞）
    C.（1﹣e，1]
    D.（﹣∞，1﹣e）∪[1，+∞）

    查看答案和解析>>

    同步练习册答案