
【题目】在数列{an}中,a1=1,an+1= ![]() (n=1,2,3,…),
(n=1,2,3,…),
(1)计算a1 , a2 , a3 , a4;
(2)猜想an的表达式,并用数学归纳法证明你的结论.
【答案】
(1)
解:∵a1=1,an+1= ![]() ,
,
∴a2= ![]() =
= ![]() ,a3=
,a3= ![]() =
= ![]() ,a4=
,a4= ![]() =
= ![]()
(2)
解:由(1)可以猜想an= ![]() .
.
用数学归纳法证明:
(ⅰ)当n=1时,a1= ![]() =1,所以当n=1时猜想成立.
=1,所以当n=1时猜想成立.
(ⅱ)假设当n=k(k∈N*)时猜想成立,即ak= ![]() ,
,
当n=k+1时,ak+1= ![]() =
= ![]() =
= ![]()
所以当n=k+1时猜想也成立.
由(ⅰ)和(ⅱ)可知,猜想对任意的n∈N*都成立.
所以an= ![]()
【解析】(1)利用数列递推式,代入计算可得结论;(2)利用(1)的结论,猜想an的表达式,再用数学归纳法证明.
【考点精析】关于本题考查的数列的通项公式,需要了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD是边长为2的正方形,平面PBC⊥底面ABCD,且 PB=PC= ![]() .
.
(Ⅰ)求证:AB⊥CP;
(Ⅱ)求点B到平面PAD的距离;
(Ⅲ)设面PAD与面PBC的交线为l,求二面角A﹣l﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一个关于平面图形的命题:如图,同一个平面内有两个边长都是a的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为 ![]() .类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .
.类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 . 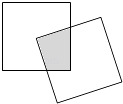
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,已知∠BAC=90°,AB=AC=1,AA1=3,点E,F分别在棱BB1 , CC1上,且C1F= ![]() C1C,BE=λBB1 , 0<λ<1.
C1C,BE=λBB1 , 0<λ<1. 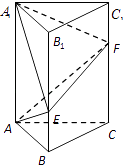
(1)当λ= ![]() 时,求异面直线AE与A1F所成角的大小;
时,求异面直线AE与A1F所成角的大小;
(2)当直线AA1与平面AEF所成角的正弦值为 ![]() 时,求λ的值.
时,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,底面是等腰直角三角形,
中,底面是等腰直角三角形, ![]() ,侧棱
,侧棱![]() ,点
,点![]() 分别为棱
分别为棱![]() 的中点,
的中点, ![]() 的重心为
的重心为![]() ,直线
,直线![]() 垂直于平面
垂直于平面![]() .
.
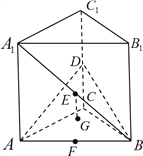
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦.
的余弦.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(Ⅰ)已知集合A={(x,y)|y=x2+2},B={(x,y)|y=6﹣x2},求A∩B; (Ⅱ)已知集合A={y|y=x2+2},B={y|y=6﹣x2},求A∩B.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com