练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在边长为2的等边中，是的中点，为线段上一动点，则的取值范围是（    ）

    A．          B．         C．            D．


    A

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    求值：sin(－1 200°)·cos 1 290°＋cos(－1 020°)·sin(－1 050°)＋tan 945°.　

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设随机变量服从正态分布,若,则(   )        

    A．3      B．      C．5     D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


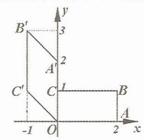
    如图，矩形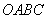在变换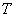的作用下变成了平行四边形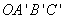，变换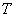所对应的矩阵为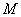，矩阵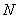是把坐标平面上的点的横坐标伸长到原来的2倍，纵坐标伸长到原来的3倍所对应的变换矩阵。 (Ⅰ)求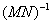；(Ⅱ)判断矩阵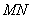是否存在特征值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    以曲线的焦点为圆心，和直线相切的圆的方程为(   )   (第4题)

         A．                 B．

         C．              D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


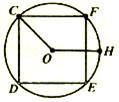
    如图，CDEF是以圆O为圆心，半径为1的圆的内接正方形，将一颗豆子随机地扔到该圆内，用A表示事件“豆子落在扇形OCFH内”（点H将劣弧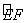二等分），则事件A发生的概率P（A）=          。               

                                                                     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数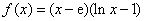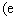为自然对数的底数）．

    （Ⅰ）求曲线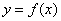在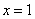处的切线方程；

    （Ⅱ）若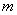是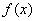的一个极值点，且点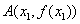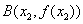，满足条件：

    .

    （ⅰ）求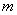的值；

    （ⅱ）求证：点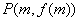，，是三个不同的点，且构成直角三角形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知正四棱柱中，.

    （Ⅰ）求证：；

    （Ⅱ）求二面角的余弦值；

    （Ⅲ）在线段上是否存在点，使得平面平面，若存在，求出的值；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


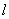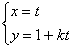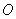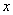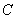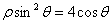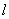    在直角坐标系中，直线的参数方程为（t为参数），以坐标原点为极点，以轴的正半轴为极轴，单位长度不变，建立极坐标系，曲线的极坐标方程为，若直线和曲线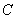相切，则实数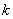的值为_________．

    查看答案和解析>>

    同步练习册答案