
【题目】已知椭圆的两个焦点为F1(﹣ ![]() ,0),F2(
,0),F2( ![]() ,0),M是椭圆上一点,若
,0),M是椭圆上一点,若 ![]()
![]() =0,|
=0,| ![]() ||
|| ![]() |=8.
|=8.
(1)求椭圆的方程;
(2)点P是椭圆上任意一点,A1、A2分别是椭圆的左、右顶点,直线PA1 , PA2与直线x= ![]() 分别交于E,F两点,试证:以EF为直径的圆交x轴于定点,并求该定点的坐标.
分别交于E,F两点,试证:以EF为直径的圆交x轴于定点,并求该定点的坐标.
【答案】
(1)
解:由题意可设椭圆的标准方程为: ![]() +
+ ![]() =1(a>b>0),
=1(a>b>0),
由 ![]()
![]() =0,∴
=0,∴ ![]() ⊥
⊥ ![]() ,设|
,设| ![]() |=m,|
|=m,| ![]() |=n.又|
|=n.又| ![]() ||
|| ![]() |=8.
|=8.
∴m2+n2= ![]() ,m+n=2a,mn=8,a2=b2+5.
,m+n=2a,mn=8,a2=b2+5.
解得:a=3,b=2.
∴椭圆的方程为 ![]() =1
=1
(2)
解:由(1)得A1(﹣3,0),A2(3,0),设P(x0,y0),则直线PA1的方程为y= ![]() (x+3),它与直线x=
(x+3),它与直线x= ![]() 的交点的坐标为E
的交点的坐标为E ![]() ,
,
直线PA2的方程为:y= ![]() (x﹣3),它与直线x=
(x﹣3),它与直线x= ![]() 的交点的坐标为F
的交点的坐标为F ![]() .
.
再设以EF为直径的圆交x轴于点Q(m,0),则QE⊥QF,
从而kQEkQF=﹣1,即 ![]() ×
× ![]() ×
× ![]() =﹣
=﹣ ![]() ,
,
即 ![]() =﹣
=﹣ ![]() ,又
,又 ![]() =9
=9 ![]() .
.
∴ ![]() =1,解得m=
=1,解得m= ![]() ±1.
±1.
故以EF为直径的圆交x轴于定点,该定点的坐标为 ![]() .
.

【解析】(1)由题意可设椭圆的标准方程为: ![]() +
+ ![]() =1(a>b>0),由
=1(a>b>0),由 ![]()
![]() =0,可得
=0,可得 ![]() ⊥
⊥ ![]() ,设|
,设| ![]() |=m,|
|=m,| ![]() |=n.又|
|=n.又| ![]() ||
|| ![]() |=8.可得m2+n2=
|=8.可得m2+n2= ![]() ,m+n=2a,mn=8,a2=b2+5.解出即可得出.(2)由(1)得A1(﹣3,0),A2(3,0),设P(x0 , y0),则直线PA1的方程为y=
,m+n=2a,mn=8,a2=b2+5.解出即可得出.(2)由(1)得A1(﹣3,0),A2(3,0),设P(x0 , y0),则直线PA1的方程为y= ![]() (x+3),它与直线x=
(x+3),它与直线x= ![]() 的交点的坐标为E,直线PA2的方程为:y=
的交点的坐标为E,直线PA2的方程为:y= ![]() (x﹣3),它与直线x=
(x﹣3),它与直线x= ![]() 的交点的坐标为F.再设以EF为直径的圆交x轴于点Q(m,0),则QE⊥QF,可得kQEkQF=﹣1,又
的交点的坐标为F.再设以EF为直径的圆交x轴于点Q(m,0),则QE⊥QF,可得kQEkQF=﹣1,又 ![]() =9
=9 ![]() .即可得出.
.即可得出.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是数列
是数列![]() 的前n项和,
的前n项和,![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)对于正整数![]() ,已知
,已知![]() 成等差数列,求正整数
成等差数列,求正整数![]() 的值;
的值;
(3)设数列![]() 前n项和是
前n项和是![]() ,且满足:对任意的正整数n,都有等式
,且满足:对任意的正整数n,都有等式![]() 成立.求满足等式
成立.求满足等式![]() 的所有正整数n.
的所有正整数n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某赛季,甲、乙两名篮球运动员都参加了![]() 场比赛,比赛得分情况如下(单位:分)
场比赛,比赛得分情况如下(单位:分)
甲:![]()
乙:![]()

(1)根据得分情况记录,作出两名篮球运动员得分的茎叶图,并根据茎叶图,对甲、乙两运动员得分作比较,写出两个统计结论;
(2)设甲篮球运动员![]() 场比赛得分平均值
场比赛得分平均值![]() ,将
,将![]() 场比赛得分
场比赛得分![]() 依次输入如图所示的程序框图进行运算,问输出的
依次输入如图所示的程序框图进行运算,问输出的![]() 大小为多少?并说明
大小为多少?并说明![]() 的统计学意义;
的统计学意义;
(3)如果从甲、乙两位运动员的![]() 场得分中,各随机抽取一场不少于
场得分中,各随机抽取一场不少于![]() 分的得分,求甲的得分大于乙的得分的概率.
分的得分,求甲的得分大于乙的得分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}为公差不为0的等差数列,满足a1=5,且a2 , a9 , a30成等比数列.
(1)求{an}的通项公式;
(2)若数列{bn}满足 ![]() ﹣
﹣ ![]() =an(n∈N*),且b1=
=an(n∈N*),且b1= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某淘宝商城在2017年前7个月的销售额![]() (单位:万元)的数据如下表,已知
(单位:万元)的数据如下表,已知![]() 与
与![]() 具有较好的线性关系.
具有较好的线性关系. 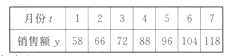
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)分析该淘宝商城2017年前7个月的销售额的变化情况,并预测该商城8月份的销售额.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
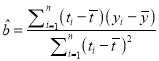 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|x2﹣x﹣6≤0}, ![]() ,那么集合A∩(UB)=( )
,那么集合A∩(UB)=( )
A.[﹣2,4)
B.(﹣1,3]
C.[﹣2,﹣1]
D.[﹣1,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点 ![]() 到点
到点 ![]() 的距离比它到直线
的距离比它到直线 ![]() 的距离小
的距离小 ![]() ,记动点
,记动点 ![]() 的轨迹为
的轨迹为 ![]() .若以
.若以 ![]() 为圆心,
为圆心, ![]() 为半径(
为半径( ![]() )作圆,分别交
)作圆,分别交 ![]() 轴于
轴于 ![]() 两点,连结并延长
两点,连结并延长 ![]() ,分别交曲线
,分别交曲线 ![]() 于
于 ![]() 两点.
两点.
(1)求曲线 ![]() 的方程;
的方程;
(2)求证:直线 ![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com