
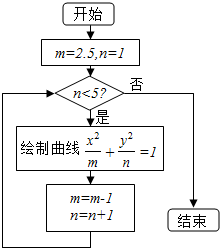
分析 模拟执行程序框图,可得绘制的曲线的方程,结合椭圆,双曲线的性质即可得解.
解答 解:模拟执行程序框图,可得绘制的曲线有:
$\frac{{x}^{2}}{2.5}+\frac{{y}^{2}}{1}=1$,椭圆的焦点在x轴上;
$\frac{{x}^{2}}{1.5}+\frac{{y}^{2}}{2}=1$,椭圆的焦点在y轴上;
$\frac{{x}^{2}}{0.5}+\frac{{y}^{2}}{3}=1$,椭圆的焦点在y轴上;
$\frac{{x}^{2}}{-0.5}+\frac{{y}^{2}}{4}$=1,双曲线的焦点在y轴上,
故答案为:3.
点评 本题主要考查了循环结构的程序框图,考查了双曲线的简单性质,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
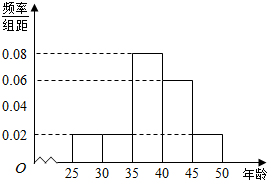 某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示,下表是年龄的频率分布表.
某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示,下表是年龄的频率分布表.| 区间 | [25,30) | [30,35) | [35.40) | [40,45) | [45,50) |
| 人数 | 25 | a | b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
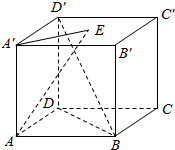 如图,已知正方体ABCD-A′B′C′D′,点E是上底面A′B′C′D′的中心,取向量$\overrightarrow{AB}$、$\overrightarrow{AD}$、$\overrightarrow{AA′}$为基底的基向量,在下列条件下,分别求x、y、z的值
如图,已知正方体ABCD-A′B′C′D′,点E是上底面A′B′C′D′的中心,取向量$\overrightarrow{AB}$、$\overrightarrow{AD}$、$\overrightarrow{AA′}$为基底的基向量,在下列条件下,分别求x、y、z的值查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com