
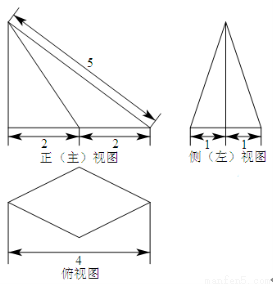
一个四棱锥的底面为菱形,其三视图如图所示,则这个四棱锥的体积是 .
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数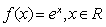 的图象与
的图象与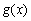 的图象关于直线
的图象关于直线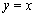 对称。
对称。
(Ⅰ)若直线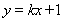 与
与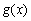 的图像相切, 求实数
的图像相切, 求实数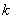 的值;
的值;
(Ⅱ)判断曲线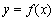 与曲线
与曲线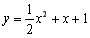 公共点的个数.
公共点的个数.
(Ⅲ)设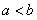 ,比较
,比较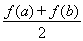 与
与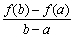 的大小, 并说明理由.
的大小, 并说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年广东省广州市毕业班综合测试一理科数学试卷(解析版) 题型:解答题
已知双曲线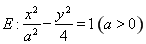 的中心为原点
的中心为原点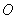 ,左、右焦点分别为
,左、右焦点分别为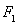 、
、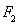 ,离心率为
,离心率为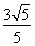 ,点
,点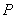 是直线
是直线 上任意一点,点
上任意一点,点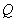 在双曲线
在双曲线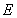 上,且满足
上,且满足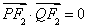 .
.
(1)求实数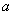 的值;
的值;
(2)证明:直线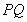 与直线
与直线 的斜率之积是定值;
的斜率之积是定值;
(3)若点 的纵坐标为
的纵坐标为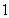 ,过点
,过点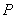 作动直线
作动直线 与双曲线右支交于不同的两点
与双曲线右支交于不同的两点 、
、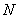 ,在线段
,在线段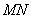 上去异于点
上去异于点 、
、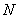 的点
的点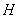 ,满足
,满足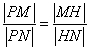 ,证明点
,证明点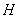 恒在一条定直线上.
恒在一条定直线上.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷2练习卷(解析版) 题型:解答题
过椭圆Γ: =1(a>b>0)右焦点F2的直线交椭圆于A,B两点,F1为其左焦点,已知△AF1B的周长为8,椭圆的离心率为
=1(a>b>0)右焦点F2的直线交椭圆于A,B两点,F1为其左焦点,已知△AF1B的周长为8,椭圆的离心率为 .
.
(1)求椭圆Γ的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆Γ恒有两个交点P,Q,且 ⊥
⊥ ?若存在,求出该圆的方程;若不存在,请说明理由.
?若存在,求出该圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷2练习卷(解析版) 题型:选择题
已知a,b是平面向量,若a⊥(a-2b),b⊥(b-2a),则a与b的夹角是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷6练习卷(解析版) 题型:选择题
某苗圃基地为了解基地内甲、乙两块地种植的同一种树苗的长势情况,从两块地各随机抽取了10株树苗,用茎叶图表示上述两组数据,对两块地抽取树苗的高度的平均数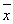 甲、
甲、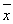 乙和中位数y甲、y乙进行比较,下面结论正确的是( )
乙和中位数y甲、y乙进行比较,下面结论正确的是( )

A.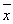 甲>
甲>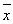 乙,y甲>y乙 B.
乙,y甲>y乙 B. 甲<
甲<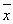 乙,y甲<y乙
乙,y甲<y乙
C. 甲<
甲<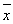 乙,y甲>y乙 D.
乙,y甲>y乙 D. 甲>
甲>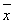 乙,y甲<y乙
乙,y甲<y乙
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com