
已知圆C的参数方程为 (θ为参数),以原点为极点,x轴的正半轴为极轴建立极坐标系,直线的极坐标方程为ρsin θ+ρcos θ=1,则直线截圆C所得的弦长是________.
(θ为参数),以原点为极点,x轴的正半轴为极轴建立极坐标系,直线的极坐标方程为ρsin θ+ρcos θ=1,则直线截圆C所得的弦长是________.
科目:高中数学 来源: 题型:
每一个父母都希望自己的孩子能升上比较理想的中学,于是就催生了“择校热”,这样“择校”的结果就导致了学生在路上耽误的时间增加了.若某生由于种种原因,每天只能6∶15骑车从家出发到学校,途径5个路口,这5个路口将家到学校分成了6个路段,每个路段的骑车时间是10分钟(通过路口的时间忽略不计),假定他在每个路口遇见红灯的概率均为 ,且该生只在遇到红灯或到达学校才停车.对每个路口遇见红灯的情况统计如下:
,且该生只在遇到红灯或到达学校才停车.对每个路口遇见红灯的情况统计如下:
| 红灯 | 1 | 2 | 3 | 4 | 5 |
| 等待时间(秒) | 60 | 60 | 90 | 30 | 90 |
(1)设学校规定7∶20后(含7∶20)到校即为迟到,求这名学生迟到的概率;
(2)设ξ表示该学生第一次停车时已经通过的路口数,求它的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆C1的参数方程为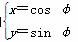 (φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C2的极坐标方程为ρ=2cos
(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C2的极坐标方程为ρ=2cos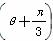 .
.
(1)将圆C1的参数方程化为普通方程,将圆C2的极坐标方程化为直角坐标方程;
(2)圆C1、C2是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
一盒中有12个乒乓球,其中9个新的,3个旧的,从盒中任取3个球来用,用完后装回盒中,此时盒中旧球个数X是一个随机变量,其分布列为P(X),则P(X=4)的值为( )
A. B.
B.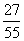 C.
C.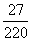 D.
D.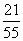
查看答案和解析>>
科目:高中数学 来源: 题型:
某餐厅供应盒饭,每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种,现在餐厅准备了6种不同的荤菜,若要保证每位顾客有100种以上的不同选择,则餐厅至少还需准备不同的素菜品多少种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com