
分析 (1)求解$f'(x)=\frac{2x-e}{x^2}$,利用导数判断即可;
(2))$g(x)=f(x)-x=2lnx+\frac{m}{x}-x(x>0)$,求解导数$g'(x)=\frac{2}{x}-\frac{m}{x^2}-1=\frac{{-{x^2}+2x-m}}{x^2}=\frac{{-{{(x-1)}^2}+1-m}}{x^2}$,利用不等式求解即可.
(3)分类讨论0<m<1时,当$0<x<1-\sqrt{1-m}$时,g'(x)<0;当$1-\sqrt{1-m}≤x<1+\sqrt{1-m}$时,g'(x)≥0;当$x≥1+\sqrt{1-m}$时,g'(x)≤0;当m≥1时,g(x)=f(x)-x在(0,+∞)上单调递减,即可的出结论.
解答 解:(1)当m=e时,$f(x)=2lnx+\frac{e}{x}$,$f'(x)=\frac{2x-e}{x^2}$,
当$x<\frac{e}{2}$时,f'(x)<0;$x=\frac{e}{2}$时,f'(x)=0;当$x>\frac{e}{2}$时,f'(x)>0.
所以,$x=\frac{e}{2}$时,f(x)取得最小值$f(\frac{e}{2})=2ln\frac{e}{2}+2=4-2ln2$.
(2)$g(x)=f(x)-x=2lnx+\frac{m}{x}-x(x>0)$,$g'(x)=\frac{2}{x}-\frac{m}{x^2}-1=\frac{{-{x^2}+2x-m}}{x^2}=\frac{{-{{(x-1)}^2}+1-m}}{x^2}$,
1m≥12时,g'(x)≤03,g(x)=f(x)-x4在(0,+∞)5单调递减.
(3)证明:0<m<1时,1-m>0,$1-\sqrt{1-m}>0$,$g'(x)=\frac{{-(x-1+\sqrt{1-m})(x-1-\sqrt{1-m})}}{x^2}$,
当$0<x<1-\sqrt{1-m}$时,g'(x)<0;当$1-\sqrt{1-m}≤x<1+\sqrt{1-m}$时,g'(x)≥0;
当$x≥1+\sqrt{1-m}$时,g'(x)≤0.
即0<m<1时,g(x)=f(x)-x在$(0\;,1-\sqrt{1-m})$和$[1+\sqrt{1-m}\;,+∞)$上单调递减,
在$[1-\sqrt{1-m}\;,\;1+\sqrt{1-m})$上单调递增.
由(2)知,当m≥1时,g(x)=f(x)-x在(0,+∞)上单调递减,
所以,当m≥1时,对任意b>a>0,f(b)-b<f(a)-a,
即对任意b>a>0,$\frac{f(b)-f(a)}{b-a}<1$.
点评 本题综合考察了函数不等式,方程的运用,利用导数解决问题的能力,分类讨论解决不等式问题,难度较大.


科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{5π}{8}\;,\;\;-\frac{9π}{16}]$ | B. | $(-\frac{5π}{4}\;,\;\;-\frac{9π}{8}]$ | C. | $[-\frac{5π}{8}\;,\;\;-\frac{9π}{16}]$ | D. | $[-\frac{5π}{4}\;,\;\;-\frac{9π}{8}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | b>c>a | C. | c>b>a | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
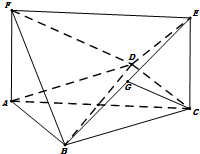 四边形ABCD是菱形,ACEF是矩形,平面ACEF⊥平面ABCD,AB=2AF=2,∠BAD=60°,G是BE的中点.
四边形ABCD是菱形,ACEF是矩形,平面ACEF⊥平面ABCD,AB=2AF=2,∠BAD=60°,G是BE的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com