
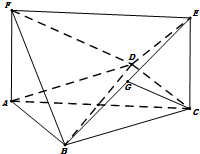
 四边形ABCD是菱形,ACEF是矩形,平面ACEF⊥平面ABCD,AB=2AF=2,∠BAD=60°,G是BE的中点.
四边形ABCD是菱形,ACEF是矩形,平面ACEF⊥平面ABCD,AB=2AF=2,∠BAD=60°,G是BE的中点.分析 (Ⅰ)根据线面平行的判定定理或者面面平行的性质定理即可证明:CG∥平面BDF
(Ⅱ)建立空间坐标系,求出平面的法向量,利用向量法即可求二面角E-BF-D的余弦值.
解答 ( I) 证法一:设AC∩BD=O,BF的中点为H,因为G是BE的中点,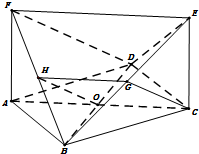 $GH∥EF∥AC,GH=\frac{1}{2}AC=OC$,
$GH∥EF∥AC,GH=\frac{1}{2}AC=OC$,
∴OCGH是平行四边形∴CG∥OH,CG?平面BDF,
OH?平面BDF,
∴CG∥平面BDF
证法二:因为G是BE的中点,$2\overrightarrow{CG}=\overrightarrow{CB}+\overrightarrow{CE}=\overrightarrow{DA}+\overrightarrow{AF}=\overrightarrow{DF}$,
∴CG∥DF,
∵CG?平面BDF,DF?平面BDF,
∴CG∥平面BDF
( II)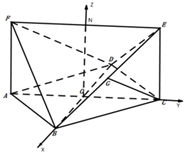
设EF的中点为N,ACEF是矩形,ON⊥AC,平面ACEF⊥平面ABCD,
∴ON⊥面ABCD∴ON⊥AC,ON⊥BD
四边形ABCD是菱形,
∴AC⊥BD,
以O为原点,OB所在直线为x轴,OC所在直线为Y轴,ON所在直线为Z轴 建立空间直角坐标系,
AB=2,AF=1,∠BAD=60°,
则$\overrightarrow{DB}=({2,0,0}),\overrightarrow{BF}=({-1,-\sqrt{3},1}),\overrightarrow{EF}=({0,-2\sqrt{3},0})$
平面BEF的法向量为$\overrightarrow{n_1}=({{x_1},{y_1},{z_1}})$,平面BDF的法向量为$\overrightarrow{n_2}=({{x_2},{y_2},{z_2}})$,
$\left\{{\begin{array}{l}{\overrightarrow{n_1}•\overrightarrow{EF}=0}\\{\overrightarrow{n_1}•\overrightarrow{BF}=0}\end{array}}\right.⇒\left\{{\begin{array}{l}{-2\sqrt{3}{y_1}=0}\\{-{x_1}-\sqrt{3}{y_1}+{z_1}=0}\end{array}}\right.$令z1=1,则$\overrightarrow{n_1}=({1,0,1})$,
由$\left\{{\begin{array}{l}{\overrightarrow{n_2}•\overrightarrow{DB}=0}\\{\overrightarrow{n_2}•\overrightarrow{BF}=0}\end{array}}\right.⇒\left\{{\begin{array}{l}{2{x_2}=0}\\{-{x_2}-\sqrt{3}{y_2}+{z_2}=0}\end{array}}\right.⇒\overrightarrow{n_2}=({0,1,\sqrt{3}})$
设二面角 E-BF-D的大小为θ
则$cosθ=|cos<\overrightarrow{{n_1},}\overrightarrow{n_2}>|=|{\frac{{\sqrt{3}}}{{\sqrt{2}×2}}}|=\frac{{\sqrt{6}}}{4}$,
则二面角E-BF-D的余弦值是$\frac{\sqrt{6}}{4}$.
点评 本题主要考查空间线面平行的判断以及二面角的求解,利用线面平行的判定定理或面面平行的性质定理以及建立空间坐标系,求出平面的法向量,利用向量法是解决二面角的关键.考查学生的运算和推理能力.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优分 | 非优分 | 总计 | |
| 男生 | |||
| 女生 | |||
| 总计 | 50 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 钝角三角形 | C. | 锐角三角形 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com