
| A. | 直角三角形 | B. | 钝角三角形 | C. | 锐角三角形 | D. | 不确定 |
分析 运用两边平方,结合向量的平方即为模的平方,设△ABC的三个内角A,B,C所对的边为a,b,c,可得k2a2-2kcacosB+c2-b2≥0,运用判别式小于等于0,化简整理,结合正弦定理和正弦函数的值域,可得三角形的形状.
解答 解:|$\overrightarrow{OA}$-$\overrightarrow{OB}$-k$\overrightarrow{BC}$|≥|$\overrightarrow{AO}$-$\overrightarrow{CO}$|,
即为|$\overrightarrow{BA}$-k$\overrightarrow{BC}$|≥|$\overrightarrow{AC}$|,
两边平方可得,$\overrightarrow{BA}$2+k2$\overrightarrow{BC}$2-2k$\overrightarrow{BA}$•$\overrightarrow{BC}$≥$\overrightarrow{AC}$2,
设△ABC的三个内角A,B,C所对的边为a,b,c,
即有c2+k2a2-2kcacosB≥b2,
即k2a2-2kcacosB+c2-b2≥0,
由题意可得△=4c2a2cos2B-4a2(c2-b2)≤0,
化为b2≤c2-c2cos2B,
即为b≤csinB,
由正弦定理可得b≤bsinC,
则sinC≥1,但sinC≤1,则sinC=1,可得C=90°.
即三角形ABC为直角三角形.
故选:A.
点评 本题考查向量不等式恒成立问题的解法,考查三角形的形状判断和正弦定理的运用,运用向量的平方即为模的平方,以及二次不等式恒成立问题的解法是解题的关键,属于中档题.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:解答题
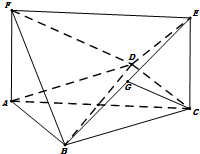 四边形ABCD是菱形,ACEF是矩形,平面ACEF⊥平面ABCD,AB=2AF=2,∠BAD=60°,G是BE的中点.
四边形ABCD是菱形,ACEF是矩形,平面ACEF⊥平面ABCD,AB=2AF=2,∠BAD=60°,G是BE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{11}$ | B. | $\frac{10}{11}$ | C. | $\frac{9}{10}$ | D. | $\frac{11}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | $\frac{4}{5}$ | C. | $-\frac{4}{5}$ | D. | $-\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com