
分析 (1)根据对数函数的定义得到关于a的方程,求出a的值,根据f(1)=1求出b的值即可;
(2)根据(1)求出f(x)的解析式,从而求出f(x)的最小值即可.
解答 解:(1)依题意得$\left\{\begin{array}{l}{a^2}-3a+3=1\\ a>0且a≠1\end{array}\right.$;
∴a=2,
又f(1)=1,
∴log2(b-2)=1,
∴b=4;
(2)$f(x)={log_2}({4^x}-{2^x})x∈[1,3]$
=${log_2}[{({2^x}-\frac{1}{2})^2}-\frac{1}{4}]$,
令$u(x)={({2^x}-\frac{1}{2})^2}-\frac{1}{4}$由于x∈[1,3],
∴2≤2x≤8,
∴u(x)在[1,3]上是增加的,
∴当x=1时$u{(x)_{min}}={(2-\frac{1}{2})^2}-\frac{1}{4}=2$,
∴f(x)min=log22=1.
点评 本题考查了对数函数的性质,考查函数的单调性、最值问题,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
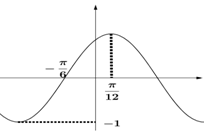 已知f(x)=Asin(ωx+φ)(A>0ω>0,$|φ|<\frac{π}{2}$,x∈R)在一个周期的图象如图所示,当$f(x)=\frac{1}{2}$时,$cos(2x-\frac{π}{6})$=( )
已知f(x)=Asin(ωx+φ)(A>0ω>0,$|φ|<\frac{π}{2}$,x∈R)在一个周期的图象如图所示,当$f(x)=\frac{1}{2}$时,$cos(2x-\frac{π}{6})$=( )| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
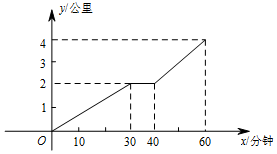 从甲同学家到乙同学家的中途有一个公园,甲、乙两家离公园入口都是2公里,甲从10点钟出发前往乙同学家,如图所示是甲同学从自己家出发到乙家经过的路程y(公里)和时间x(分钟)的关系.根据图象,回答下列问题:
从甲同学家到乙同学家的中途有一个公园,甲、乙两家离公园入口都是2公里,甲从10点钟出发前往乙同学家,如图所示是甲同学从自己家出发到乙家经过的路程y(公里)和时间x(分钟)的关系.根据图象,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 随着k的增大而增大 | |
| B. | 随着k的增大而减小 | |
| C. | 是一个与k无关的常数 | |
| D. | 有时随k增大而增大,有时随k增大而减小 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com