
分析 (1)由正弦定理和正弦函数的性质化简已知的等式,由商的关系即可证明;
(2)由题意和两角和的正切公式列出方程,结合(1)和A是锐角求出tanA的值,由同角三角函数的基本关系求出cosA,由余弦定理求出a的值.
解答 证明:(1)由bsinCcosA-4csinAcosB=0得,
bsinCcosA=4csinAcosB,…(1分)
由正弦定理得,sinBsinCcosA=4sinCsinAcosB,
又sinC≠0,则sinB•cosA=4sinA•cosB…(3分)
所以$\frac{sinB}{cosB}=\frac{4sinA}{cosA}$,即tanB=4tanA;
解:(2)因为tan(A+B)=-3,所以$\frac{tanA+tanB}{1-tanA•tanB}=-3$,
由(1)得,$\frac{5tanA}{1-4ta{n}^{2}A}=-3$,
解得tanA=$\frac{3}{4}$或tanA=$-\frac{1}{3}$,
又A为锐角,则$tanA=\frac{3}{4}$,
所以$\left\{\begin{array}{l}{\frac{sinA}{cosA}=\frac{3}{4}}\\{si{n}^{2}A+co{s}^{2}A=1}\end{array}\right.$,解得$cosA=\frac{4}{5}$…(9分)
由余弦定理得,a2=b2+c2-2bccosA
=$25+9-2×5×3×\frac{4}{5}=10$,
即$a=\sqrt{10}$…(10分)
点评 本题考查了正弦定理、余弦定理,同角三角函数的基本关系,以及两角和的正切公式等,注意内角的范围,考查化简、变形能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
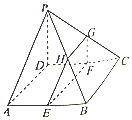 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为菱形,.点分E,F,G,H别是棱AB,CD,PC,PB上共面的四点,且BC∥EF.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为菱形,.点分E,F,G,H别是棱AB,CD,PC,PB上共面的四点,且BC∥EF. 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 2 | C. | 6$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
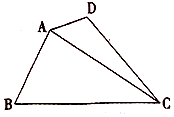 如图,四边形ABCD中,∠BAD=135°,∠ADC=120°,∠BCD=45°,∠ABC=60°,BC=$\sqrt{3}$,则线段AC长度的取值范围是( )
如图,四边形ABCD中,∠BAD=135°,∠ADC=120°,∠BCD=45°,∠ABC=60°,BC=$\sqrt{3}$,则线段AC长度的取值范围是( )| A. | $[{\sqrt{2},\sqrt{3}})$ | B. | $[{\frac{3}{2},\sqrt{3}})$ | C. | $({\sqrt{2},\sqrt{3}})$ | D. | $({\frac{3}{2},\sqrt{3}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∧q | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $9\sqrt{3}$ | B. | 9 | C. | 18 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com