
| A. | 2$\sqrt{3}$ | B. | 2 | C. | 6$\sqrt{3}$ | D. | 6 |
分析 利用定积分求出λ=9,由q>0,且$\frac{{a}_{4}+λ{a}_{2}}{{a}_{3}}$=$\frac{{a}_{4}+9{a}_{2}}{{a}_{3}}$=q+$\frac{9}{q}$,利用均值定理能求出$\frac{{a}_{4}+λ{a}_{2}}{{a}_{3}}$的最小值.
解答 解:∵λ=${∫}_{0}^{3}$x2dx=($\frac{1}{3}{x}^{3}$)${|}_{0}^{3}$=9,
数列{an}是各项均为正数的等比数列,
∴q>0,且$\frac{{a}_{4}+λ{a}_{2}}{{a}_{3}}$=$\frac{{a}_{4}+9{a}_{2}}{{a}_{3}}$=$\frac{{a}_{1}{q}^{3}+9{{a}_{1}q}^{\;}}{{a}_{1}{q}^{2}}$=$\frac{{q}^{2}+9}{q}$=q+$\frac{9}{q}$≥2$\sqrt{q•\frac{9}{q}}$=6.
当且仅当q=$\frac{9}{q}$,即q=3时,$\frac{{a}_{4}+λ{a}_{2}}{{a}_{3}}$取最小值为6.
故选:D.
点评 本题考查等比数列中代数式和的最小值的求法,涉及到定积分、等比数列、均值定值,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
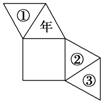 某人用如图所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①、②、③处应依次写上( )
某人用如图所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①、②、③处应依次写上( )| A. | 快、新、乐 | B. | 乐、新、快 | C. | 新、乐、快 | D. | 乐、快、新 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (2,+∞) | C. | (-∞,0)∪(2,+∞) | D. | (-∞,0)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最大值为$\frac{2}{3}$,无最小值 | B. | 有最大值为$-\frac{1}{3}$,无最小值 | ||
| C. | 有最小值为$-\frac{1}{3}$,无最大值 | D. | 有最小值为$\frac{2}{3}$,无最大值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{0,\frac{1}{2}})$ | B. | [0,1] | C. | $({\frac{1}{2},1}]$ | D. | $({\frac{1}{2},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com