
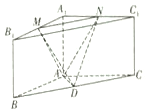
 如下图所示的三棱柱ABC-A1B1C1中,棱AA1⊥底面A1B1C1,AB=AC=AA1,∠ABC=30°,M,N,D分别是A1B1,A1C1,BC的中点.
如下图所示的三棱柱ABC-A1B1C1中,棱AA1⊥底面A1B1C1,AB=AC=AA1,∠ABC=30°,M,N,D分别是A1B1,A1C1,BC的中点.分析 (Ⅰ)取B1C1的中点D1,连接DD1,A1D1,可得A1D1⊥B1C1,再由三角形中位线定理可得MN∥B1C1,则MN⊥A1D1,由AA1⊥底面A1B1C1,得AA1⊥MN,再由线面垂直的判定可得MN⊥平面A1ADD1,则MN⊥AD;
(Ⅱ)以A为坐标原点,建立如下图所示的空间直角坐标系为O-xyz(点O与点A重合),求出所用点的坐标,进一步求出平面ADM与平面ADN的一个法向量,由两法向量所成角的余弦值求得二面角M-AD-N的余弦值.
解答 (Ⅰ)证明:如下图,取B1C1的中点D1,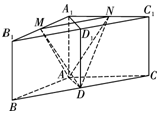
连接DD1,A1D1,
在三棱柱ABC-A1B1C1中,由AB=AC,得A1B1=A1C1,∴A1D1⊥B1C1,
∵M,N分别是A1B1,A1C1的中点,∴MN∥B1C1,得MN⊥A1D1,
∵AA1⊥底面A1B1C1,MN?平面A1B1C1,∴AA1⊥MN,
又∵AA1∩A1D1=A1,∴MN⊥平面A1ADD1,
∵AD?平面A1ADD1,
∴MN⊥AD;
(Ⅱ)解:设AA1=2,作AH∥BC,
以A为坐标原点,建立如下图所示的空间直角坐标系为O-xyz(点O与点A重合),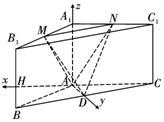
则A(0,0,0),A1(0,0,2),
由题意,D为BC的中点,AB=AC=AA1,∠ABC=30°,
∴D(0,1,0),$B(\sqrt{3},\;\;1,\;\;0)$,${B_1}(\sqrt{3},\;\;1,\;\;2)$,$C(-\sqrt{3},\;\;1,\;\;0)$,${C_1}(-\sqrt{3},\;\;1,\;\;2)$,
由M,N分别是A1B1,A1C1的中点,得$M(\frac{\sqrt{3}}{2},\frac{1}{2},2)$,$N({-\frac{{\sqrt{3}}}{2},\;\;\frac{1}{2},\;\;2})$,
∴$\overrightarrow{AD}=(0,\;\;1,\;\;0)$,$\overrightarrow{AM}=({\frac{{\sqrt{3}}}{2},\;\;\frac{1}{2},\;\;2})$,$\overrightarrow{AN}=({-\frac{{\sqrt{3}}}{2},\;\;\frac{1}{2},\;\;2})$,
设平面ADM的一个法向量为$\overrightarrow n=(x,\;\;y,\;\;z)$,∴$\overrightarrow n⊥\overrightarrow{AD}$,$\overrightarrow n⊥\overrightarrow{AM}$,
则$\left\{\begin{array}{l}y=0,\;\;\\ \frac{{\sqrt{3}}}{2}x+\frac{1}{2}y+2z=0,\;\;\end{array}\right.$
取$z=-\sqrt{3}$,则y=0,x=4,
于是$\overrightarrow n=(4,\;\;0,\;\;-\sqrt{3})$.
同理可得平面ADN的一个法向量为$\overrightarrow m=(4,\;\;0,\;\;\sqrt{3})$.
设二面角M-AD-N的平面角为θ,
由题意知,θ为锐角,∴$cosθ=|cos<\overrightarrow n,\;\;\overrightarrow m>|$=$|{\frac{\overrightarrow n\;•\;\overrightarrow m}{|\overrightarrow n||\overrightarrow m|}}|$=$|{\frac{{4×4+0-\sqrt{3}×\sqrt{3}}}{{\sqrt{19}×\sqrt{19}}}}|=\frac{13}{19}$,
因此,二面角M-AD-N的余弦值为$\frac{13}{19}$.
点评 本题考查直线与平面垂直的判定,考查空间想象能力和思维能力,训练了利用空间向量求二面角的平面角,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
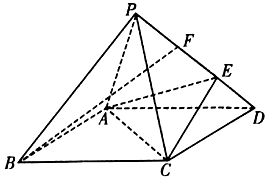 19、如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=PC=1,$PB=PD=\sqrt{2}$,E为线段PD上一点,且PE=2ED.
19、如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=PC=1,$PB=PD=\sqrt{2}$,E为线段PD上一点,且PE=2ED.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | [2,4) | C. | [2,+∞) | D. | [2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{10}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | cos50° | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
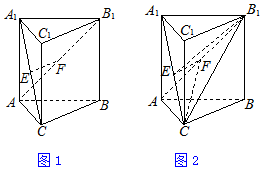 如图,三棱柱ABC-A1B1C1中,侧棱AA1与底面垂直,∠ACB=90°,AC=BC,AA1=AB=2,E,F分别是A1C,AB1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1与底面垂直,∠ACB=90°,AC=BC,AA1=AB=2,E,F分别是A1C,AB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
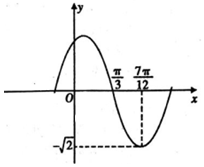 函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,若方程f(x)=a在x∈[-$\frac{π}{4}$,$\frac{π}{2}$]上有两个不相等的实数根,则a的取值范围是( )
函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,若方程f(x)=a在x∈[-$\frac{π}{4}$,$\frac{π}{2}$]上有两个不相等的实数根,则a的取值范围是( )| A. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$) | B. | [-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$) | C. | [-$\frac{\sqrt{6}}{2}$,$\sqrt{2}$) | D. | [$\frac{\sqrt{6}}{2}$,$\sqrt{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com