
分析 任取x1,x2∈[$\sqrt{2}$,+∞),且x1<x2,通过作差比较f(x1)与f(x2)的大小,根据增函数的定义,只需说明f(x1)<f(x2)即可
解答 解:证明:任取x1,x2∈[$\sqrt{2}$,+∞),且x1<x2,
则f(x1)-f(x2)(x1$+\frac{2}{{x}_{1}}$)-(x2$+\frac{2}{{x}_{2}}$)=$\frac{({x}_{1}-{x}_{2})({x}_{1}{x}_{2}-2)}{{x}_{1}{x}_{2}}$,
因为$\sqrt{2}$≤x1<x2,所以x1-x2<0,x1x2>2,
所以f(x1)-f(x2)<0,即f(x1)<f(x2),
所以f(x)=x+$\frac{2}{x}$在[$\sqrt{2}$,+∞)上为增函数.
点评 本题考查函数单调性的证明,属基础题,单调性的证明方法主要有:定义法;导数法,要熟练掌握.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
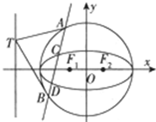 已知椭圆 C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,动点P在椭圆上,且使得∠F1PF2=90°的点P恰有两个,动点P到焦点F1的距离的最大值为2+$\sqrt{2}$.
已知椭圆 C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,动点P在椭圆上,且使得∠F1PF2=90°的点P恰有两个,动点P到焦点F1的距离的最大值为2+$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com