
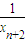 的直线交曲线C于另一点An+1(xn+1,yn+1),点列{An}的横坐标构成数列{xn},其中x1=
的直线交曲线C于另一点An+1(xn+1,yn+1),点列{An}的横坐标构成数列{xn},其中x1=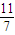 .
.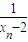 +
+ ,求证:数列{bn}是等比数列;
,求证:数列{bn}是等比数列;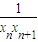 ,利用kn=
,利用kn= ,即可得到xn与xn+1的关系式;
,即可得到xn与xn+1的关系式;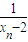 +
+ ,可得bn+1=-2(
,可得bn+1=-2(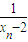 +
+ ),从而可得数列{bn}是等比数列.
),从而可得数列{bn}是等比数列.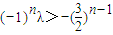 恒成立,对n讨论,即可得到结论.
恒成立,对n讨论,即可得到结论.
 ,∴-
,∴- =
=
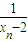 +
+ ,∴bn+1=
,∴bn+1=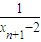 +
+ =
=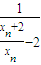 +
+ =-2(
=-2(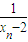 +
+ ),
), ,∴b1=-2
,∴b1=-2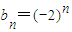 ,则cn+1>cn成立等价于cn+1-cn=2×3n+3λ×(-2)n>0恒成立
,则cn+1>cn成立等价于cn+1-cn=2×3n+3λ×(-2)n>0恒成立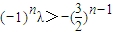 恒成立
恒成立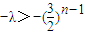 ,∴
,∴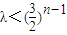 ,∴λ<1;
,∴λ<1;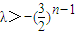 ,∴
,∴
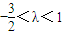


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 1 |
| xn+2 |
| 11 |
| 7 |
| 1 |
| xn-2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| xn+1 | ||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| xn+2 |
| 11 |
| 7 |
| 1 |
| xn-2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| xn+2 |
| 11 |
| 7 |
| 1 |
| xn-2 |
| 1 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com