
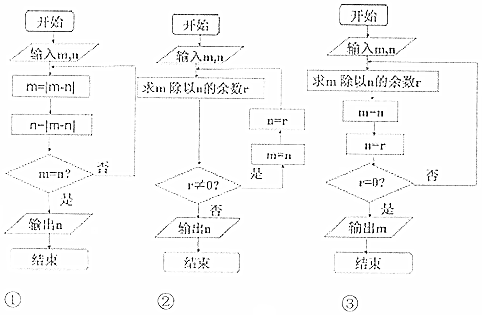
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
分析 先写出用辗转相除法和更相减损术求最大公约数的算法,模拟执行流程图,即可得解.
解答 解:①辗转相除法是求两个自然数的最大公约数的一种方法,也叫欧几里得算法,算法如下:
第一步,输入两个正整数m,n,
第二步,m除以n的余数是r,
接下来,将原来的除数作为新的被除数,原来的余数作为除数,继续上面的过程,直到余数r=0,
退出程序,输出两个正整数的最大公约数m.
②更相减损术,是出自《九章算术》的一种求最大公约数的算法,算法如下:
第一步:任意给定两个正整数;判断它们是否都是偶数.若是,则用2约简;若不是则执行第二步.
第二步:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数.继续这个操作,直到所得的减数和差相等为止.
则第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数.
结合算法,模拟执行流程图,即可得解能够实现两个正整数的最大公约数的算法有3个.
故选:C.
点评 辗转相除法与更相减损术的区别:
(1)都是求最大公因数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显.
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{3\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1f(x2)>x2f(x1) | B. | x1f(x2)<x2f(x1) | C. | x1f(x2)=x2f(x1) | D. | x1f(x1)=x2f(x2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(0)<f(5) | B. | f(-1)<f(3) | C. | f(3)>f(2) | D. | f(2)>f(0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
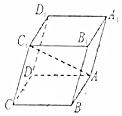 如图,已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,侧棱AA1长为3,且∠A1AB=∠A1AD=120°,则AC1=$\sqrt{5}$.
如图,已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,侧棱AA1长为3,且∠A1AB=∠A1AD=120°,则AC1=$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{9}$ | B. | $\frac{5}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
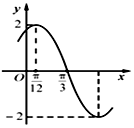 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将f(x)图象上的所有点向右平移$\frac{π}{6}$个单位得到函数g(x)的图象,则函数g(x)的单调递增区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将f(x)图象上的所有点向右平移$\frac{π}{6}$个单位得到函数g(x)的图象,则函数g(x)的单调递增区间为( )| A. | [kπ-$\frac{π}{4}$,kπ+$\frac{π}{4}$],k∈Z | B. | [2kπ-$\frac{π}{4}$,2kπ+$\frac{π}{4}$],k∈Z | ||
| C. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z | D. | [2kπ-$\frac{π}{3}$,2kπ+$\frac{π}{6}$],k∈Z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com