
【题目】一个多面体的直观图及三视图如图所示:(其中M,N分别是AF,BC的中点). 
(1)求证:MN∥平面CDEF;
(2)求多面体A﹣CDEF的体积.
【答案】
(1)解:由三视图可知,该多面体是底面为直角三角形的直三棱柱ADE﹣BCF,
且AB=BC=BF=2,DE=CF=2 ![]() ,∴∠CBF=
,∴∠CBF= ![]() .
.
证明:取BF的中点G,连接MG、NG,
由M,N分别为AF,BC的中点可得,NG∥CF,MG∥EF,
∴平面MNG∥平面CDEF,又MN平面MNG,
∴MN∥平面CDEF
(2)解:取DE的中点H.
∵AD=AE,∴AH⊥DE,
在直三棱柱ADE﹣BCF中,
平面ADE⊥平面CDEF,
平面ADE∩平面CDEF=DE.∴AH⊥平面CDEF.
∴多面体A﹣CDEF是以AH为高,以矩形CDEF为底面的棱锥,在△ADE中,AH= ![]() .
.
S矩形CDEF=DEEF=4 ![]() ,
,
∴棱锥A﹣CDEF的体积为
V= ![]() S矩形CDEFAH=
S矩形CDEFAH= ![]() ×4
×4 ![]() ×
× ![]() =
= ![]()

【解析】由三视图可知,该多面体是底面为直角三角形的直三棱柱ADE﹣BCF,且底面是一个直角三角形,由三视图中所标数据易计算出三棱柱中各棱长的值.(1)取BF的中点G,连接MG、NG,利用中位线的性质结合线面平行的充要条件,易证明结论(2)多面体A﹣CDEF的体积是一个四棱锥,由三视图易求出棱锥的底面面积和高,进而得到棱锥的体积.
【考点精析】掌握简单空间图形的三视图和直线与平面平行的判定是解答本题的根本,需要知道画三视图的原则:长对齐、高对齐、宽相等;平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


科目:高中数学 来源: 题型:
【题目】已知f(x)=lnx+x2﹣bx.
(1)若函数f(x)在其定义域内是增函数,求b的取值范围;
(2)当b=﹣1时,设g(x)=f(x)﹣2x2 , 求证函数g(x)只有一个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A、B、C所对边的长分别为a、b、c,且有2sinBcosA=sinAcosC+cosAsinC. (Ⅰ)求角A的大小;
(Ⅱ)若b=2,c=1,D为BC的中点,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求证:方程![]() 有实根;
有实根;
(2)![]() 在
在![]() 上是单调递减函数,求实数
上是单调递减函数,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 的解集为空集,求所有满足条件的实数
的解集为空集,求所有满足条件的实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了探索一种新的教学模式,进行了一项课题实验,甲班为实验班,乙班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,测试成绩的分组区间为![]() 80,90
80,90![]() 、
、![]() 90,100
90,100![]() 、
、![]() 100,110
100,110![]() 、
、![]() 110,120
110,120![]() 、
、![]() 120,130
120,130![]() ,由此得到两个班测试成绩的频率分布直方图:
,由此得到两个班测试成绩的频率分布直方图:
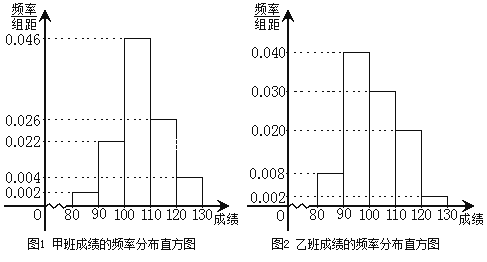
(1)完成下面2×2列联表,你能有97.5![]() 的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
成绩小于100分 | 成绩不小于100分 | 合计 | |
甲班 |
|
| 50 |
乙班 |
|
| 50 |
合计 |
|
| 100 |
(2)根据所给数据可估计在这次测试中,甲班的平均分是105.8,请你估计乙班的平均分,并计算两班平均分相差几分?
附:
![]() ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5. 024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数
上是增函数![]() 若函数
若函数![]() ,利用上述性质,
,利用上述性质,
![]() Ⅰ
Ⅰ![]() 当
当![]() 时,求
时,求![]() 的单调递增区间
的单调递增区间![]() 只需判定单调区间,不需要证明
只需判定单调区间,不需要证明![]() ;
;
![]() Ⅱ
Ⅱ![]() 设
设![]() 在区间
在区间![]() 上最大值为
上最大值为![]() ,求
,求![]() 的解析式;
的解析式;
![]() Ⅲ
Ⅲ![]() 若方程
若方程![]() 恰有四解,求实数a的取值范围.
恰有四解,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com