
【题目】求下列不等的解集
(1)求不等式 ![]() ≥1的实数解;
≥1的实数解;
(2)解关于x的不等式 ![]() >1.
>1.
【答案】
(1)解:不等式 ![]() ≥1
≥1 ![]() ,由|x+1|≥|x+2|(x+1)2≥(x+2)2,化为2x+3≤0,解得x≤﹣
,由|x+1|≥|x+2|(x+1)2≥(x+2)2,化为2x+3≤0,解得x≤﹣ ![]() ,由x+2≠0,解得x≠﹣2.
,由x+2≠0,解得x≠﹣2.
∴不等式的解集为{x|x≤﹣ ![]() 且x≠﹣2}
且x≠﹣2}
(2)解:不等式(x﹣2)[(a﹣1)x﹣(a﹣2)]>0 (I)
①当a>1时,(I)3(x﹣2)(x﹣ ![]() )>0,
)>0,
因 ![]() =1﹣
=1﹣ ![]() <2,所以不等式解集为{x|x>2或x<
<2,所以不等式解集为{x|x>2或x< ![]() }
}
②当a<1时,(I)(x﹣2)(x﹣ ![]() )<0
)<0
若0<a<1时, ![]() >2时,不等式的解集为{x|2<x<
>2时,不等式的解集为{x|2<x< ![]() }
}
若a<0时, ![]() <2时,不等式解集为{x|
<2时,不等式解集为{x| ![]() <x<2}
<x<2}
若a=0时,不等式的解集为.
③当a=1时,原不等式x﹣2>0,解集为{x|x>2}
综上当a>1时,不等式解集为{x|x>2或x< ![]() };当a=1时,解集为{x|x>2};若0<a<1时,不等式的解集为{x|2<x<
};当a=1时,解集为{x|x>2};若0<a<1时,不等式的解集为{x|2<x< ![]() };若a=0时,不等式的解集为;若a<0时,不等式解集为:{x|
};若a=0时,不等式的解集为;若a<0时,不等式解集为:{x| ![]() <x<2}
<x<2}
【解析】(1)不等式式 ![]() ≥1
≥1 ![]() ,由|x+1|≥|x+2|(x+1)2≥(x+2)2 , 展开解出即可.(2)不等式(x﹣2)[(a﹣1)x﹣(a﹣2)]>0,分类讨论,结合而成不等式的解法,即可得出结论.
,由|x+1|≥|x+2|(x+1)2≥(x+2)2 , 展开解出即可.(2)不等式(x﹣2)[(a﹣1)x﹣(a﹣2)]>0,分类讨论,结合而成不等式的解法,即可得出结论.
【考点精析】认真审题,首先需要了解绝对值不等式的解法(含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号).


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】记max{a,b}= ![]() ,设M=max{|x﹣y2+4|,|2y2﹣x+8|},若对一切实数x,y,M≥m2﹣2m都成立,则实数m的取值范围是 .
,设M=max{|x﹣y2+4|,|2y2﹣x+8|},若对一切实数x,y,M≥m2﹣2m都成立,则实数m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,四点
,四点![]() ,
,![]() ,
,![]() ,
,![]() 中恰有两个点为椭圆
中恰有两个点为椭圆![]() 的顶点,一个点为椭圆
的顶点,一个点为椭圆![]() 的焦点.
的焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)若斜率为1的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且
,且![]() ,求直线
,求直线![]() 方程.
方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小李从网上购买了一件商品,快递员计划在下午5:00-6:00之间送货上门,已知小李下班到家的时间为下午5:30-6:00.快递员到小李家时,如果小李未到家,则快递员会电话联系小李.若小李能在10分钟之内到家,则快递员等小李回来;否则,就将商品存放在快递柜中.则小李需要去快递柜收取商品的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合P={x|x2﹣x﹣6<0},Q={2a≤x≤a+3}.
(1)若P∪Q=P,求实数a的取值范围;
(2)若P∩Q=,求实数a的取值范围;
(3)若P∩Q={x|0≤x<3},求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2019·朝鲜中学]在如图所示的程序框图中,有这样一个执行框![]() ,其中的函数关系式为
,其中的函数关系式为![]() ,程序框图中的
,程序框图中的![]() 为函数
为函数![]() 的定义域.
的定义域.
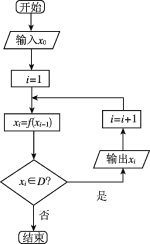
(1)若输入![]() ,请写出输出的所有
,请写出输出的所有![]() 的值;
的值;
(2)若输出的所有![]() 都相等,试求输入的初始值
都相等,试求输入的初始值![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个多面体的直观图及三视图如图所示:(其中M,N分别是AF,BC的中点). 
(1)求证:MN∥平面CDEF;
(2)求多面体A﹣CDEF的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com