
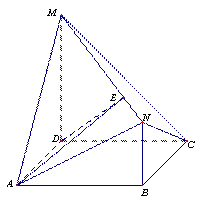
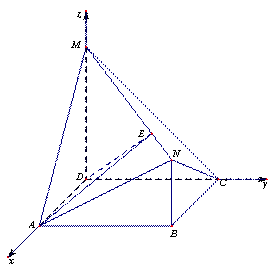
如图,四边形ABCD是边长为2的正方形,MD⊥平面ABCD,NB∥MD,且NB=1,MD=2;(Ⅰ)求证:AM∥平面BCN;
(Ⅱ)求AN与平面MNC所成角的正弦值;
(Ⅲ)E为直线MN上一点,且平面ADE⊥平面MNC,求 的值.
的值.
解:(Ⅰ)∵ABCD是正方形,
∴BC∥AD.
∵BCË平面AMD,AD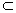 平面AMD,
平面AMD,
∴BC∥平面AMD.
∵NB∥MD,
∵NBË平面AMD,MD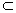 平面AMD,
平面AMD,
∴NB∥平面AMD.
∵NB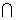 BC=B,NB
BC=B,NB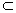 平面BCN, BC
平面BCN, BC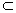 平面BCN,
平面BCN,
∴平面AMD∥平面BCN
∵AM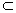 平面AMD,
平面AMD,
∴AM∥平面BCN
(也可建立直角坐标系,证明AM垂直平面BCN的法向量,酌情给分)
(Ⅱ)
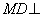 平面ABCD,ABCD是正方形,所以,可选点D为原点,DA,DC,DM所在直线分别为x,y,z轴,建立空间直角坐标系(如图)
平面ABCD,ABCD是正方形,所以,可选点D为原点,DA,DC,DM所在直线分别为x,y,z轴,建立空间直角坐标系(如图)
 则
则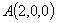 ,
,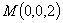 ,
,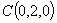 ,
,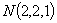 .
.

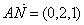 ,
,
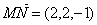 ,
,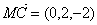 ,
,
设平面MNC的法向量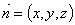 ,
,
则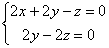 ,令
,令 ,则
,则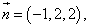
设AN与平面MNC所成角为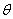 ,
,

 . ……9分
. ……9分
(Ⅲ)设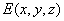 ,
,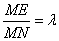 ,
,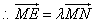 ,
,
又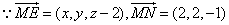 ,
,
 E点的坐标为
E点的坐标为 ,
,
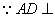 面MDC,
面MDC,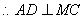 ,
,
欲使平面ADE⊥平面MNC,只要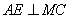 ,
,
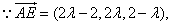
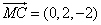 ,
,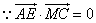
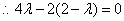 ,
,
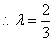

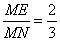 .
.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
已知中心在原点,焦点在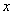 轴上的椭圆
轴上的椭圆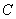 过点
过点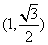 ,离心率为
,离心率为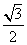 ,点
,点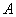 为其右顶点.过点
为其右顶点.过点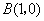 作直线
作直线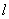 与椭圆
与椭圆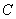 相交于
相交于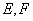 两点,直线
两点,直线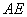 ,
, 与直线
与直线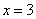 分别交于点
分别交于点 ,
,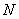 .
.
(Ⅰ)求椭圆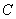 的方程;
的方程;
(Ⅱ)求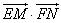 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
100个个体分成10组,编号后分别为第1组:00,01,02,…,09;第2组:10,11,12,…,19;…;第10组:90,91,92,…,99.现在从第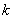 组中抽取其号码的个位数与
组中抽取其号码的个位数与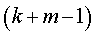 的个位数相同的个体,其中
的个位数相同的个体,其中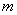 是第1组随机抽取的号码的个位数,则当
是第1组随机抽取的号码的个位数,则当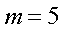 时,从第7组中抽取的号码是( )
时,从第7组中抽取的号码是( )
A.61 B.65 C.71 D.75
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com