
| a+m |
| b+m |
| a |
| b |
| 1 |
| a-b |
| 1 |
| b-c |
| 1 |
| c-a |
| A、1 | B、2 | C、3 | D、4 |
| a+m |
| b+m |
| a |
| b |
| a+x |
| b+x |
| 1 |
| a-b |
| 1 |
| b-c |
| 1 |
| c-a |
| a+m |
| b+m |
| a |
| b |
| a+x |
| b+x |
| a-b |
| b+x |
| a+m |
| b+m |
| a |
| b |
| a+x |
| b+x |
| 1 |
| a-b |
| 1 |
| b-c |
| 1 |
| c-a |
| 1 |
| b-c |
| 1 |
| c-a |
| 1 |
| a-b |
| 1 |
| b-c |
| 1 |
| c-a |


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:高中数学 来源: 题型:
A.x2≠y2![]() x≠y或x≠-y
x≠y或x≠-y
B.命题“若a、b都是偶数,则a+b是偶数”的逆否命题是“若a+b不是偶数,则a、b都不是偶数”
C.若“p或q”为假则“非p且非q”为真
D.“|x|<2”是“x2-x-6<0”的必要非充分条件
查看答案和解析>>
科目:高中数学 来源:2014届湖北省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
下列命题中正确的是( )
A.命题“若 ,则
,则 ”的否命题为“若
”的否命题为“若 ,则
,则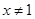 ”
”
B.“ ”是“
”是“ ”的必要不充分条件
”的必要不充分条件
C.命题“ ,使得
,使得 ”的否定是“
”的否定是“ ,均有
,均有 ”
”
D.命题“在 中,若
中,若 ,则
,则 ”的逆否命题为真命题
”的逆否命题为真命题
查看答案和解析>>
科目:高中数学 来源:2012-2013学年黑龙江高三上期末考试理科数学试卷(解析版) 题型:选择题
设m、n是两条不同的直线, 、β是两个不同的平面,则下列命题中正确的是
、β是两个不同的平面,则下列命题中正确的是
A.若m∥n,m∥ ,则n∥
,则n∥
B.若 ⊥β,m∥
⊥β,m∥ ,则m⊥β
,则m⊥β
C.若 ⊥β,m⊥β,则m∥
⊥β,m⊥β,则m∥
D.若m⊥n,m⊥ ,n⊥β,则
,n⊥β,则 ⊥β
⊥β
查看答案和解析>>
科目:高中数学 来源:2014届浙江省高二9月质量检测文科数学试卷(解析版) 题型:选择题
已知m,n是两条不同直线,α、β、γ是三个不同平面.下列命题中正确的是
A.若m∥α,n∥α,则m∥n B.若α⊥γ,β⊥γ,则α∥β
C.若m∥α,m∥β,则α∥β D.若m⊥α,n⊥α,则m∥n
查看答案和解析>>
科目:高中数学 来源:2010年河南大学附属中学(本部)高一上学期期中考试数学卷 题型:选择题
若函数 唯一的一个零点同时在区间(0,16),(0,8),(0,4),(0,2)内,那么下列命题中正确的是(
).
唯一的一个零点同时在区间(0,16),(0,8),(0,4),(0,2)内,那么下列命题中正确的是(
).
A. 函数 在区间(0,1)内有零点
B. 函数
在区间(0,1)内有零点
B. 函数 在区间(0,1)或(1,2)内有零点
在区间(0,1)或(1,2)内有零点
C. 函数 在区间(2,16)内无零点 D. 函数
在区间(2,16)内无零点 D. 函数 在区间(1,16)内无零点
在区间(1,16)内无零点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com