
|
| OM |
| OA |
|
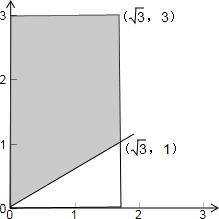 解:满足约束条件
解:满足约束条件
|
| 3 |
| 3 |
| OA |
| 3 |
| OM |
| OM |
| OA |
| 3 |
| OM |
| OA |
| 3 |
| OM |
| OA |
| OM |
| OA |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| A、0 | B、1 | C、2 | D、3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
①两条直线互相平行的充要条件是它们的斜率相等而截距不等;②方程(2x+y-3)+λ(x-y+2)=0(λ为常数)表示经过两直线2x+y-3=0与x-y+2=0交点的所有直线;③过点M(x0,y0),且与直线ax+by+c=0(ab≠0)平行的直线方程是a(x-x0)+b(y-y0)=0;④两条平行直线3x-2y+5=0与?6x-4y+8=0间的距离是d=![]() .
.
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2009年广东省深圳外国语学校高考数学二模试卷(理科)(解析版) 题型:选择题
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三下学期模拟预测文科数学试卷(解析版) 题型:解答题
设不等边三角形ABC的外心与重心分别为M、G,若A(-1,0),B(1,0)且MG//AB.
(Ⅰ)求三角形ABC顶点C的轨迹方程;
(Ⅱ)设顶点C的轨迹为D,已知直线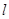 过点(0,1)并且与曲线D交于P、N两点,若O为坐标原点,满足OP⊥ON,求直线
过点(0,1)并且与曲线D交于P、N两点,若O为坐标原点,满足OP⊥ON,求直线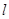 的方程.
的方程.
【解析】
第一问因为设C(x,y)(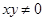 )
)
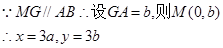 ……3分
……3分
∵M是不等边三解形ABC的外心,∴|MA|=|MC|,即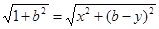 (2)
(2)
由(1)(2)得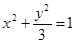 .所以三角形顶点C的轨迹方程为
.所以三角形顶点C的轨迹方程为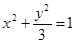 ,
,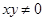 .…6分
.…6分
第二问直线l的方程为y=kx+1
由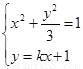 消y得
消y得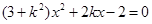 。 ∵直线l与曲线D交于P、N两点,∴△=
。 ∵直线l与曲线D交于P、N两点,∴△=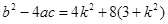 ,
,
又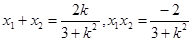 ,
,
∵ ,∴
,∴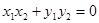
 得到直线方程。
得到直线方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com