
【题目】已知函数f(x)的值满足f(x)<0,对任意实数x,y都有f(xy)=f(x)f(y),且f(﹣1)=1,f(27)=9,当0<x<1时,f(x)∈(0,1).
(1)求f(1)的值,判断f(x)的奇偶性并证明;
(2)判断f(x)在(0,+∞)上的单调性,并给出证明;
(3)若a≥0且f(a+1)≤ ![]() ,求a的取值范围.
,求a的取值范围.
【答案】
(1)解:令x=y=﹣1,可得f(1)=1…(2分)令y=﹣1,则f(﹣x)=f(x)f(﹣1),∵f(﹣1)=1,∴f(﹣x)=f(x),f(x)为偶函数
(2)解:f(x)在(0,+∞)上是增函数,
证明如下:若x>0,则f(x)=f( ![]() )≥0.
)≥0.
若存在x0>0,使得f(x0)=0,则f(27)=f( ![]() )=f(
)=f( ![]() )×f(x0)=0与已知矛盾,
)×f(x0)=0与已知矛盾,
∴当x>0时,f(x)>0
设:0<x1<x2,∴ ![]() ,由题设知
,由题设知 ![]()
且 ![]() ,∴
,∴ ![]() …(8分)
…(8分)
![]() ∴f(x1)<f(x2),
∴f(x1)<f(x2),
故f(x)在(0,+∞)上是增函数
(3)解:∵f(27)=9,而f(27)=f(3×9)=f(3)×f(9)=[f(3)]3∴ ![]() ∵
∵ ![]()
∴f(a+1)≤f(3),∴a+1≤3,a≥00≤a≤2.
∴a的取值范围:[0,2]
【解析】(1)利用赋值法,令y=﹣1,代入抽象函数表达式即可证明函数的奇偶性;(2)先证明当x>0时,f(x)>0,再利用已知和单调函数的定义,证明函数f(x)在[0,+∞)上的单调性;(3)先利用赋值法求得f(3)= ![]() 再利用函数的单调性解不等式即可
再利用函数的单调性解不等式即可


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某市环保局从市区2017年上半年每天的PM2.5监测数据中随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶)
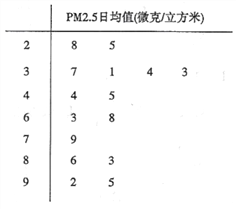
(1)从这15天的数据中任取一天,求这天空气质量达到一级的概率;
(2)从这15天的数据中任取3天的数据,记![]() 表示其中空气质量达到一级的天数,求
表示其中空气质量达到一级的天数,求![]() 的分布列;
的分布列;
(3)以这15天的PM2.5的日均值来估计一年的空气质量情况,(一年按360天来计算),则一年中大约有多少天的空气质量达到一级.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员400人,每人每年可创利10万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.05万元,但公司需付下岗职员每人每年2万元的生活费,并且该公司正常运转所需人数不得小于现有职员的 ![]() ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的倾斜角为
的倾斜角为![]() 且经过点
且经过点![]() ,以原点
,以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,与直角坐标系
轴正半轴为极轴,与直角坐标系![]() 取相同的长度单位,建立极坐标系,设曲线
取相同的长度单位,建立极坐标系,设曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 有公共点,求
有公共点,求![]() 的取值范围;
的取值范围;
(2)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),0<β<α<π.
=(cosβ,sinβ),0<β<α<π.
(1)若| ![]() ﹣
﹣ ![]() |=
|= ![]() ,求证:
,求证: ![]() ⊥
⊥ ![]() ;
;
(2)设c=(0,1),若 ![]() +
+ ![]() =c,求α,β的值.
=c,求α,β的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2(a+2)x+a2 , g(x)=﹣x2+2(a﹣2)x﹣a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)},(其中max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A﹣B=( )
A.a2﹣2a﹣16
B.a2+2a﹣16
C.﹣16
D.16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com