
| A. | fn($\frac{1}{3}$)>1 | B. | fn($\frac{1}{3}$)=1 | C. | fn($\frac{1}{3}$)<1 | D. | 与n的大小有关 |
分析 求出函数的解析式,利用错位相减法,求出fn($\frac{1}{3}$),即可得出结论.
解答 解:由已知f1(-1)=-a1=-1,所以a1=1
f2(-1)=-a1+a2=2,所以a2=3,
f3(-1)=-a1+a2-a3=-3,所以a3=5
∵(-1)n+1•an+1=fn+1(-1)-fn(-1)=(-1)n+1•(n+1)-(-1)n•n
∴an+1=(n+1)+n
即an+1=2n+1
所以对于任意的n=1,2,3,an=2n-1,
∴fn(x)=x+3x2+5x3+…+(2n-1)xn
∴fn($\frac{1}{3}$)=$\frac{1}{3}$+3($\frac{1}{3}$)2+5($\frac{1}{3}$)3+…+(2n-1)($\frac{1}{3}$)n ①
$\frac{1}{3}$fn($\frac{1}{3}$)=($\frac{1}{3}$)2+3($\frac{1}{3}$)3+5($\frac{1}{3}$)4+…+(2n-1)($\frac{1}{3}$)n+1 ②
①─②,得
$\frac{2}{3}$fn($\frac{1}{3}$)=($\frac{1}{3}$)+2($\frac{1}{3}$)3+2($\frac{1}{3}$)4+…+2($\frac{1}{3}$)n-(2n-1)($\frac{1}{3}$)n+1,
=$\frac{2}{3}$-$\frac{2n-2}{3}$($\frac{1}{3}$)n,
∴fn($\frac{1}{3}$)=1-$\frac{n-1}{{3}^{n}}$
又n=1,2,3,故fn($\frac{1}{3}$)<1.
点评 本题考查数列的通项与求和,考查错位相减法的运用,考查学生的计算能力,确定数列的通项,正确求和是关键.


科目:高中数学 来源: 题型:选择题
| A. | ln3-ln2 | B. | 2ln3-2ln2 | C. | 2ln2-ln3 | D. | 4ln2-2ln3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
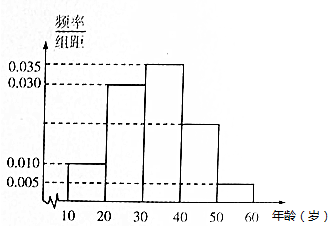 为了调查市民对某活动的认可程度,研究人员对其所在地区年龄在10~60岁间的n位市民作出调查,并将统计结果绘制成频率分布直方图如图所示,若被调查的年龄在20~30岁间的市民有480人,则可估计被调查的年龄在40~50岁间的市民有320人.
为了调查市民对某活动的认可程度,研究人员对其所在地区年龄在10~60岁间的n位市民作出调查,并将统计结果绘制成频率分布直方图如图所示,若被调查的年龄在20~30岁间的市民有480人,则可估计被调查的年龄在40~50岁间的市民有320人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
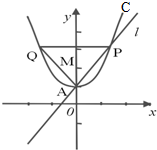 已知二次函数y=ax2+1的图象为抛物线C,过顶点A(0,1)的直线l与抛物线C相交于另外一点P,点Q为抛物线C上另外一点,且点M(0,m)到直线l的距离为1.
已知二次函数y=ax2+1的图象为抛物线C,过顶点A(0,1)的直线l与抛物线C相交于另外一点P,点Q为抛物线C上另外一点,且点M(0,m)到直线l的距离为1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
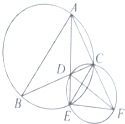 如图,在△ABC中,∠BAC的平分线交BC于点D,交△ABC的外接圆于点E,延长AC交△DCE的外接圆于点F,DF=$\sqrt{14}$.
如图,在△ABC中,∠BAC的平分线交BC于点D,交△ABC的外接圆于点E,延长AC交△DCE的外接圆于点F,DF=$\sqrt{14}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com