
| A. | ln3-ln2 | B. | 2ln3-2ln2 | C. | 2ln2-ln3 | D. | 4ln2-2ln3 |
分析 先利用定积分表示出点A为区域Ω内任意一点,点A落在曲线C下方的面积,然后求出区域Ω的面积,最后根据几何概型的概率公式进行求解即可.
解答 解:0≤x≤1时,y=$\frac{1}{{x}^{2}+3x+2}$>0,且函数单调递减,
x=0时,y=$\frac{1}{2}$,x=1时,y=$\frac{1}{6}$,点A为区域Ω内任意一点,
则点A为区域Ω内任意一点,点A落在曲线C下方的面积为${∫}_{0}^{1}$$\frac{1}{{x}^{2}+3x+2}$dx=${∫}_{0}^{1}$$\frac{1}{x+1}$dx-${∫}_{0}^{1}$$\frac{1}{x+2}$dx=[ln(x+1)-ln(x+2)]${|}_{0}^{1}$=2ln2-ln3,
∵区域Ω的面积为$\frac{1}{2}$,
∴所求概率为4ln2-2ln3.
故选:D.
点评 本题主要考查了利用定积分表示曲边三角形的面积,以及几何概型的概率公式,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (±4,0) | B. | (0,±3) | C. | (±3,0) | D. | (0,±4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
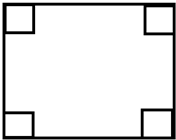 用一边长为1米,另一边长为a(0<a≤1)米的矩形铁皮做一个无盖的容器,先在四角分别截去一个长为x的小正方形,然后把四边翻折90°角,再焊接而成,设该容器的容积为f(x).
用一边长为1米,另一边长为a(0<a≤1)米的矩形铁皮做一个无盖的容器,先在四角分别截去一个长为x的小正方形,然后把四边翻折90°角,再焊接而成,设该容器的容积为f(x).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | fn($\frac{1}{3}$)>1 | B. | fn($\frac{1}{3}$)=1 | C. | fn($\frac{1}{3}$)<1 | D. | 与n的大小有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com