
分析 利用向量的平方与其模长的平方相等,得到关于$|{\overrightarrow b}|$的方程解出.
解答 解:因为向量$\overrightarrow a,\overrightarrow b$夹角为45°,且$|{\overrightarrow a}|=1,|{2\overrightarrow a-\overrightarrow b}|=\sqrt{10}$,则$4{\overrightarrow{a}}^{2}-4\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}=10$,即4-2$\sqrt{2}$|$\overrightarrow{b}$|+|$\overrightarrow{b}$|2=10,解得$|{\overrightarrow b}|$=$3\sqrt{2}$,(-$\sqrt{2}$舍去);
故答案为:3$\sqrt{2}$.
点评 本题考查了平面向量的平方与模长的平方相等,通过方程思想求向量的模长.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:解答题
 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
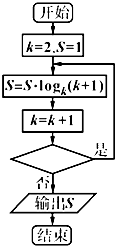
| A. | k<9? | B. | k<8? | C. | k<7? | D. | k<6? |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ln3-ln2 | B. | 2ln3-2ln2 | C. | 2ln2-ln3 | D. | 4ln2-2ln3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
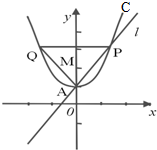 已知二次函数y=ax2+1的图象为抛物线C,过顶点A(0,1)的直线l与抛物线C相交于另外一点P,点Q为抛物线C上另外一点,且点M(0,m)到直线l的距离为1.
已知二次函数y=ax2+1的图象为抛物线C,过顶点A(0,1)的直线l与抛物线C相交于另外一点P,点Q为抛物线C上另外一点,且点M(0,m)到直线l的距离为1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com