
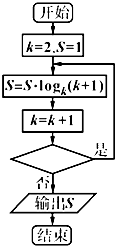
| A. | k<9? | B. | k<8? | C. | k<7? | D. | k<6? |
分析 利用二项展开式的通项公式求出展开式的通项,令x的指数为0,求出展开式的常数项,根据程序框图,写出运行结果,根据程序输出的结果是S=3,可得判断框内应填入的条件.
解答 解:∵(x+$\frac{1}{\sqrt{x}}$)3展开式中的通项为Tr+1=${C}_{3}^{r}$x3-r($\frac{1}{\sqrt{x}}$)r=${C}_{3}^{r}$x${\;}^{3-\frac{3r}{2}}$,
∴令3-$\frac{3r}{2}$=0,得r=2,可得:展开式的常数项为C32=3,
模拟程序的运行,可得
S k
第一次循环 log23 3
第二次循环 log23•log34 4
第三次循环 log23•log34•log45 5
第四次循环 log23•log34•log45•log56 6
第五次循环 log23•log34•log45•log56•log67 7
第六次循环 log23•log34•log45•log56•log67•log78=$\frac{lg3}{lg2}×\frac{lg4}{lg3}×…×\frac{lg8}{lg7}$=3 8
由题意,此时,应该不满足条件,退出循环,输出S的值为3,可得判断框中应填入的条件是k<8.
故选:B.
点评 本题考查利用二项展开式的通项公式解决二项展开式的特定项问题,考查程序框图,尤其考查循环结构,对循环体每次循环需要进行分析并找出内在规律,属于中档题.


科目:高中数学 来源: 题型:解答题
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
| 男生 | 女生 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2>k0) | 0.05 | 0.05 | 0.01 |
| K0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD⊥AB,DC∥AB,$AD=AE=DC=\frac{1}{2}AB=4$,△MDC是等边三角形,且平面MDC⊥平面ABCD.
如图,在四边形ABCD中,AD⊥AB,DC∥AB,$AD=AE=DC=\frac{1}{2}AB=4$,△MDC是等边三角形,且平面MDC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
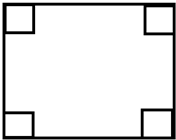 用一边长为1米,另一边长为a(0<a≤1)米的矩形铁皮做一个无盖的容器,先在四角分别截去一个长为x的小正方形,然后把四边翻折90°角,再焊接而成,设该容器的容积为f(x).
用一边长为1米,另一边长为a(0<a≤1)米的矩形铁皮做一个无盖的容器,先在四角分别截去一个长为x的小正方形,然后把四边翻折90°角,再焊接而成,设该容器的容积为f(x).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了适应市场需要,某地准备建一个圆形生猪储备基地(如图),它的附近有一条公路,从基地中心O处向东走1km是储备基地的边界上的点A,接着向东再走7km到达公路上的点B;从基地中心O向正北走8km到达公路的另一点C.现准备在储备基地的边界上选一点D,修建一条由D通往公路BC的专用线DE,求DE的最短距离.
为了适应市场需要,某地准备建一个圆形生猪储备基地(如图),它的附近有一条公路,从基地中心O处向东走1km是储备基地的边界上的点A,接着向东再走7km到达公路上的点B;从基地中心O向正北走8km到达公路的另一点C.现准备在储备基地的边界上选一点D,修建一条由D通往公路BC的专用线DE,求DE的最短距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com