
分析 (1)当a=1,对于p:x2-4x+3<0,利用一元二次不等式的解法可得实数x的取值范围.由$\frac{x-3}{x-2}<0$,化为(x-2)(x-3)<0,解得实数x的取值范围.若p∧q为真,则p真且q真,即可得出.
(2)设A={x|p(x)},B={x|q(x)}=(2,3),由p是q的必要不充分条件,可得$B\begin{array}{l}?\\≠\end{array}A$,对a分类讨论,即可得出.
解答 解:(1)当a=1,对于p:x2-4x+3<0,解得1<x<3,即p为真时实数x的取值范围是1<x<3.
由$\frac{x-3}{x-2}<0$,化为(x-2)(x-3)<0,解得2<x<3,因此q为真时实数x的取值范围是2<x<3.
若p∧q为真,则p真且q真,∴$\left\{\begin{array}{l}{1<x<3}\\{2<x<3}\end{array}\right.$,解得2<x<3,
∴实数x的取值范围是(2,3).
(2)设A={x|p(x)},B={x|q(x)}=(2,3),
∵p是q的必要不充分条件,∴$B\begin{array}{l}?\\≠\end{array}A$,
由x2-4ax+3a2<0得(x-3a)(x-a)<0,
当a>0时,A=(a,3a),有$\left\{{\begin{array}{l}{a≤2}\\{3a≥3}\end{array}}\right.$,解得1≤a≤2;
当a<0时,A=(3a,a),显然A∩B=∅,不合题意.
∴实数a的取值范围是1≤a≤2.
点评 本题考查了不等式的解法、简易逻辑的判定方法、集合之间的关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
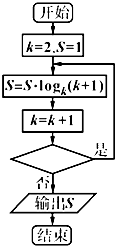
| A. | k<9? | B. | k<8? | C. | k<7? | D. | k<6? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ln3-ln2 | B. | 2ln3-2ln2 | C. | 2ln2-ln3 | D. | 4ln2-2ln3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
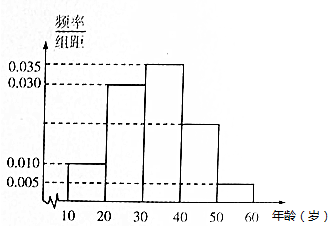 为了调查市民对某活动的认可程度,研究人员对其所在地区年龄在10~60岁间的n位市民作出调查,并将统计结果绘制成频率分布直方图如图所示,若被调查的年龄在20~30岁间的市民有480人,则可估计被调查的年龄在40~50岁间的市民有320人.
为了调查市民对某活动的认可程度,研究人员对其所在地区年龄在10~60岁间的n位市民作出调查,并将统计结果绘制成频率分布直方图如图所示,若被调查的年龄在20~30岁间的市民有480人,则可估计被调查的年龄在40~50岁间的市民有320人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com