
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
| 男生 | 女生 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2>k0) | 0.05 | 0.05 | 0.01 |
| K0 | 2.706 | 3.841 | 6.635 |
分析 (1)由题意可得非优秀学生共5人,记测评等级为合格的3人为a,b,c,尚待改进的2人为A,B,则从这5人中任选2人的所有可能结果为10个,设事件C表示“从表二的非优秀学生5人中随机选取2人,恰有1人测评等级为合格”,则C的结果为6个,根据概率公式即可求解.(2)由2×2列联表直接求解即可.
解答 解:(1)设从高一年级男生中抽出m人,则$\frac{m}{500}=\frac{45}{500+400}$,∴m=25,
∴x=25-20=5,y=20-18=2,
表2中非优秀学生共5人,记测评等级为合格的3人为a,b,c,尚待改进的2人为A,B,
则从这5人中任选2人的所有可能结果为:(a,b)(a,c)(b,c)(A,B)(a,A),(a,B),(b,A)(,b,B),(c,A)(c,B),共10种.
设事件C表示“从表二的非优秀学生5人中随机选取2人,恰有1人测评等级为合格”,
则C的结果为:(a,A),(a,B),(b,A)(,b,B),(c,A)(c,B),共6种.
∴P(C)=$\frac{6}{10}$=$\frac{3}{5}$,故所求概率为$\frac{3}{5}$.
(2)2×2列联表
| 男生 | 女生 | 总计 | |
| 优秀 | 15 | 15 | 30 |
| 非优秀 | 10 | 5 | 15 |
| 总计 | 25 | 20 | 45 |
点评 本考查了独立检验思想在实际问题中的应用,属于中档题.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案科目:高中数学 来源: 题型:选择题
| A. | ∠A>∠B的充要条件是sinA>sinB | |
| B. | ∠A>∠B的充要条件是cosA<cosB | |
| C. | ∠A>∠B的充要条件是tanA>tanB | |
| D. | ∠A>∠B的充要条件是$\frac{cosA}{sinA}<\frac{cosB}{sinB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a?α,b?β,且a∥b,则α∥β | B. | 若a?α,b?β,且a⊥b,则α⊥β | ||
| C. | 若a∥α,b?β,则a∥b | D. | 若a⊥α,b⊥β,α∥β,则a∥b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图甲,在边长为4的等边三角形ABC中,点E,F分别为AB,AC上一点,且EF∥BC,EF=2a,沿EF将三角形AEF折起,使得平面AEF⊥平面EFCB,形成一个如图乙所示的四棱锥,设O为EF的中点.
如图甲,在边长为4的等边三角形ABC中,点E,F分别为AB,AC上一点,且EF∥BC,EF=2a,沿EF将三角形AEF折起,使得平面AEF⊥平面EFCB,形成一个如图乙所示的四棱锥,设O为EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
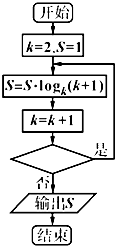
| A. | k<9? | B. | k<8? | C. | k<7? | D. | k<6? |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com