
 如图甲,在边长为4的等边三角形ABC中,点E,F分别为AB,AC上一点,且EF∥BC,EF=2a,沿EF将三角形AEF折起,使得平面AEF⊥平面EFCB,形成一个如图乙所示的四棱锥,设O为EF的中点.
如图甲,在边长为4的等边三角形ABC中,点E,F分别为AB,AC上一点,且EF∥BC,EF=2a,沿EF将三角形AEF折起,使得平面AEF⊥平面EFCB,形成一个如图乙所示的四棱锥,设O为EF的中点.分析 (Ⅰ)推导出AO⊥EF,AO⊥平面EFCB,由此能证明AO⊥BE.
(Ⅱ)取CB的中点D,以O为原点,分别以OE,OD,OA为x,y,z轴建立空间直角坐标系,利用向量法能求出二面角F-AE-B的正弦值.
解答  (本小题满分12分)
(本小题满分12分)
证明:(Ⅰ)∵△AEF为等边三角形,O为EF的中点,
∴AO⊥EF.
∵平面AEF⊥平面EFCB,平面AEF∩平面EFCB=EF,AO?平面AEF,
∴AO⊥平面EFCB,又BE?平面EFCB,
∴AO⊥BE. …(4分)
解:(Ⅱ)如图,取CB的中点D,连接OD,
以O为原点,分别以OE,OD,OA为x,y,z轴建立空间直角坐标系,
则$A(0,\;\;0,\;\;\sqrt{3}a),\;\;E(a,\;\;0,\;\;0),\;\;B(2,\;\;2\sqrt{3}-\sqrt{3}a,\;\;0)$,
∴$\overrightarrow{AE}=(a,\;\;0,\;\;-\sqrt{3}a),\;\;\overrightarrow{EB}=(2-a,\;\;2\sqrt{3}-\sqrt{3}a,\;\;0)$.
设平面AEB的法向量为$\overrightarrow{n_1}=(x,\;\;y,\;\;z)$,
则$\left\{\begin{array}{l}{\overrightarrow n_1}•\overrightarrow{AE}=ax-\sqrt{3}az=0\\{\overrightarrow n_1}•\overrightarrow{EB}=(2-a)x+(2\sqrt{3}-\sqrt{3}a)y=0\end{array}\right.$,
令$z=\sqrt{3}$,则$x=3,\;\;y=-\sqrt{3}$,$\overrightarrow{n_1}=(3,\;\;-\sqrt{3},\;\;\sqrt{3})$,
平面AEF的法向量为$\overrightarrow{n_2}=(0,\;\;1,\;\;0)$,
∴$cos?\overrightarrow{n_1},\;\;\overrightarrow{n_2}>=\frac{{\overrightarrow{n_1}•\overrightarrow{n_2}}}{{|\overrightarrow{n_1}||\overrightarrow{n_2}|}}=\frac{{-\sqrt{3}}}{{\sqrt{15}}}=-\frac{{\sqrt{5}}}{5}$,
∴二面角F-AE-B的正弦值为$\sqrt{1-\frac{1}{5}}$=$\frac{{2\sqrt{5}}}{5}$. …(12分)
点评 本题考查线线垂直的证明,考查二面角的正弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | $[{\sqrt{3},2}]$ | C. | $(-∞,-2)∪[{\sqrt{3},2}]$ | D. | $({-∞,-\sqrt{3}}]∪[{\sqrt{3},2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
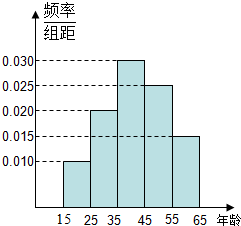 为了了解四川省各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“四川省有哪几个著名的旅游景点?”统计结果如表.
为了了解四川省各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“四川省有哪几个著名的旅游景点?”统计结果如表.| 组号 | 分组 | 回答正确的人数 | 回答正确的人数 占本组的频率 |
| 第1组 | [15,25) | a | 0.5 |
| 第2组 | [25,35) | 18 | x |
| 第3组 | [35,45) | b | 0.9 |
| 第4组 | [45,55) | 9 | 0.36 |
| 第5组 | [55,65] | 3 | y |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
| 男生 | 女生 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2>k0) | 0.05 | 0.05 | 0.01 |
| K0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 任意x∈R,f(π+x)=f(x) | B. | 任意x∈R,$f(\frac{π}{2}+x)=f(\frac{π}{2}-x)$ | ||
| C. | 不存在${x_0}∈(0,\frac{π}{2})$,使f(x0)=0 | D. | 不存在${x_0}∈(0,\frac{π}{2})$,使$f({x_0})>\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD⊥AB,DC∥AB,$AD=AE=DC=\frac{1}{2}AB=4$,△MDC是等边三角形,且平面MDC⊥平面ABCD.
如图,在四边形ABCD中,AD⊥AB,DC∥AB,$AD=AE=DC=\frac{1}{2}AB=4$,△MDC是等边三角形,且平面MDC⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com