
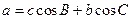 ;类比上述结论,写出下列条件下的结论:四面体P-ABC中,△ABC,△PAB,△PBC,△PCA的面积分别是
;类比上述结论,写出下列条件下的结论:四面体P-ABC中,△ABC,△PAB,△PBC,△PCA的面积分别是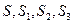 ,二面角
,二面角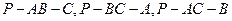 的度数分别是
的度数分别是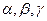 ,则
,则 ;
; 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源:不详 题型:解答题
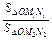 =
=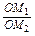 ·
·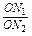 ;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是什么?这个结论正确吗?说明理由.
;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是什么?这个结论正确吗?说明理由.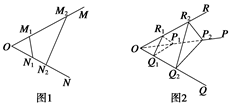
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
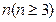 维向量,
维向量,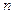 维向量可用
维向量可用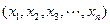 表示.设
表示.设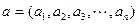 ,
,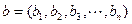 ,规定向量
,规定向量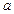 与
与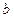 夹角
夹角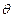 的余弦为
的余弦为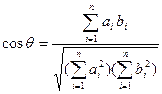 .当
.当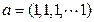 ,
,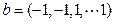 时,
时,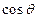 =" "
=" "  B.
B. C.
C. D.
D.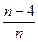
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com