
已知函数
(1)若 =1,解不等式
=1,解不等式
(2)若a=1,当 时,
时, 恒成立,求
恒成立,求 的取值范围
的取值范围
(1)见解析;(2)
【解析】
试题分析: (1)把分式不等式转化成整式不等式,注意看清分子、分母的符号;(2)解含参数的一元二次不等式分类讨论的依据:一是二次项中若含有参数应讨论是小于0,等于0,还是大于0,然后将不等式转化为二次项系数为正的形式,二是当不等式对应的方程的根个数不确定时,讨论判别式 与0的关系,三是确定无根时可直接写出解集,确定方程有两个根时,要讨论两根的大小关系,从而确定解集;(3)讨论时注意找临界条件. (4)对于恒成立的问题,常用到以下两个结论:(1)
与0的关系,三是确定无根时可直接写出解集,确定方程有两个根时,要讨论两根的大小关系,从而确定解集;(3)讨论时注意找临界条件. (4)对于恒成立的问题,常用到以下两个结论:(1) ,(2)
,(2)
试题解析:(1)∵ ,
, ,
,
∴ ,
,
∴ ,
,
∵ ,
,
∴ ,等价于
,等价于 ,
,
①当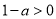 ,即
,即 时,不等式的解集为:
时,不等式的解集为: ,
,
②当 ,即
,即 时,不等式的解集为:
时,不等式的解集为: ,
,
③当 ,即
,即 时,不等式的解集为:
时,不等式的解集为: ,
,
(2)∵ ,
, ,
,

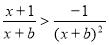
 ,显然
,显然 ,当
,当 时成立;
时成立;
当 时,不等式恒成立,可知
时,不等式恒成立,可知 ;
;
当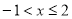 时,
时,



考点:含参数的分式不等式及恒成立问题


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源:2015届吉林省长春市高二下学期期末考试文科数学试卷(解析版) 题型:解答题
设函数 (
( ).
).
(1)求 的单调区间;(4分)
的单调区间;(4分)
(2)求所有实数 ,使
,使 对
对 恒成立.(8分)
恒成立.(8分)
(注: 为自然对数的底数)
为自然对数的底数)
查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市高二下学期期中考试文科数学试卷(解析版) 题型:选择题
已知双曲线
 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于 ,则该双曲线的方程为( )
,则该双曲线的方程为( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届吉林省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
已知函数 ,在点
,在点 处的切线方程是
处的切线方程是 (e为自然对数的底)。
(e为自然对数的底)。
(1)求实数 的值及
的值及 的解析式;
的解析式;
(2)若 是正数,设
是正数,设 ,求
,求 的最小值;
的最小值;
(3)若关于x的不等式 对一切
对一切 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省高二第一次月考数学试卷(解析版) 题型:解答题
在△ABC中,角A,B,C的对边分别为 ,且A,B,C成等差数列。
,且A,B,C成等差数列。
(1)若 ,
, ,求△ABC的面积;
,求△ABC的面积;
(2)若 成等比数列,试判断△ABC的形状。
成等比数列,试判断△ABC的形状。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省沈阳市高二上学期10月月考数学试卷(解析版) 题型:填空题
若数列{an}是等差数列,首项a1>0,a 2003+a 2004>0,a 2003·a 2004<0,则使前n项和Sn>0成立的最大自然数n是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com